Download paper with DOI
Download preprint-pdf
Authors
A. Rakotondrandisa, G. Sadaka, I. Danaila
Abstract
We present and distribute a new numerical system using classical finite elements with mesh adaptivity for computing two-dimensional liquid-solid phase-change systems involving natural convection. The programs are written as a toolbox for FreeFem++ (www.freefem.org), a free finite-element software available for all existing operating systems. The code implements a single domain approach. The same set of equations is solved in both liquid and solid phases: the incompressible Navier-Stokes equations with Boussinesq approximation for thermal effects. This model describes naturally the evolution of the liquid flow which is dominated by convection effects. To make it valid also in the solid phase, a Carman-Kozeny-type penalty term is added to the momentum equations. The penalty term brings progressively (through an artificial mushy region) the velocity to zero into the solid. The energy equation is also modified to be valid in both phases using an enthalpy (temperature-transform) model introducing a regularized latent-heat term.
Model equations are discretized using Galerkin triangular finite elements. Piecewise quadratic (P2) finite-elements are used for the velocity and piecewise linear (P1) for the pressure. For the temperature both P2 or P1 discretizations are possible. The coupled system of equations is integrated in time using a second-order Gear scheme. Non-linearities are treated implicitly and the resulting discrete equations are solved using a Newton algorithm. An efficient mesh adaptivity algorithm using metrics control is used to adapt the mesh every time step. This allows us to accurately capture multiple solid-liquid interfaces present in the domain, the boundary-layer structure at the walls and the unsteady convection cells in the liquid.
We present several validations of the toolbox, by simulating benchmark cases of increasing difficulty: natural convection of air, natural convection of water, melting of a phase-change material, a melting-solidification cycle, and, finally, a water freezing case. Other similar cases could be easily simulated with this toolbox, since the code structure is extremely versatile and the syntax very close to the mathematical formulation of the model.
FreeFem++ Toolbox
Nature of problem: The software computes 2D configurations of liquid-solid phase-change problems with convection in the liquid phase. Natural convection, melting and solidification processes are illustrated in the paper. The software can be easily modified to take into account different related physical models.
Solution method: We use a single domain approach, solving the incompressible Navier-Stokes equations with Boussinesq approximation in both liquid and solid phases. A Carman-Kozeny-type penalty term is added to the momentum equations to bring the velocity to zero into the solid phase. An enthalpy model is used in the energy equation to take into account the phase change. Discontinuous variables (latent heat, material properties) are regularized through an intermediate (mushy) region. Space discretization is based on Galerkin triangular finite elements. Piecewise quadratic (P2) finite-elements are used for the velocity and piecewise linear (P1) for the pressure. For the temperature both P2 or P1 discretizations are possible. A second order Gear scheme is used for the time integration of the coupled system of equations. Non-linear terms are treated implicitly and the resulting discrete equations are solved using a Newton algorithm. A mesh adaptivity algorithm is implemented to reduce the computational time and increase the local space accuracy when (multiple) interfaces are present.
Running time: From minutes for natural convection case to hours for melting or solidification (on a personal laptop). The water freezing case may require several days of computational time.
Supplemental material
| Test Case | Parameters | Movie |
|---|---|---|
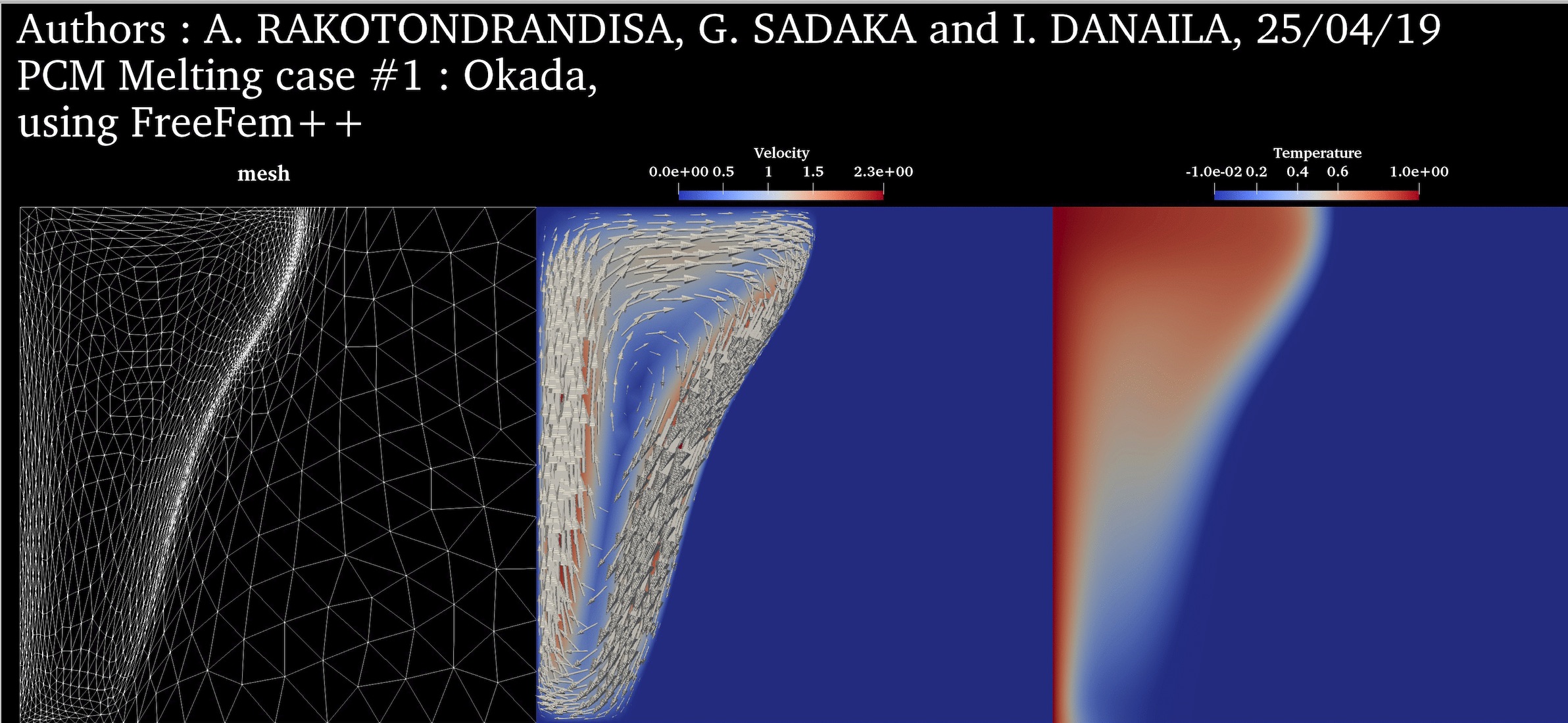 |
$Ra = 3.27 \cdot 10^5$ $Pr = 56.2$ $Ste = 0.045$ $V_{ref} = \frac{\nu_l}{H}$ |
PCM Melting Case-1: Melting of a square PCM (Okada, 1984) ➟ Download/Watch movie |
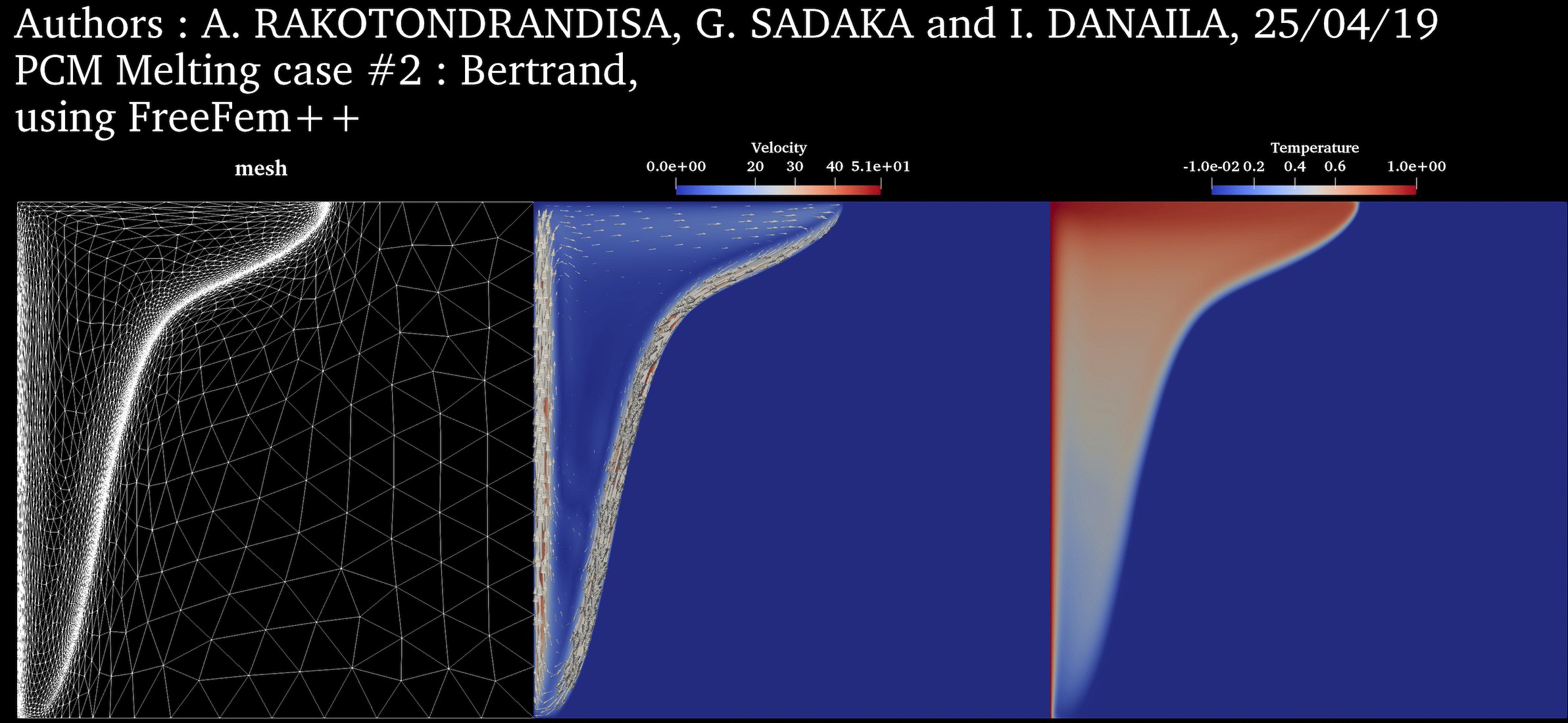 |
$Ra = 10^8$ $Pr = 50$ $Ste = 0.1$ $V_{ref} = \frac{\nu_l}{H}$ |
PCM Melting Case-2: Melting of a square PCM at high Rayleigh number (Bertrand et al., 1999) ➟ Download/Watch movie |
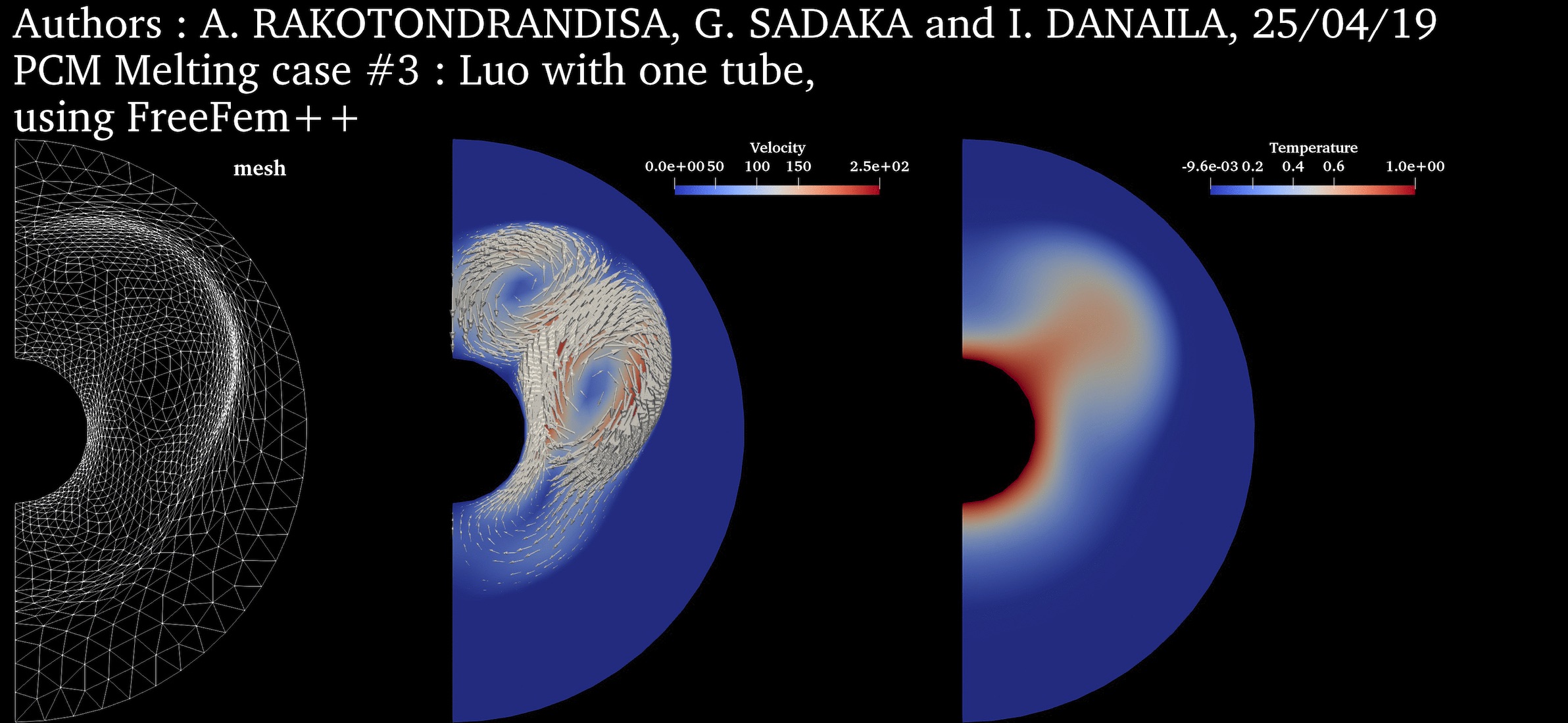 |
$Ra = 5 \cdot 10^4$ $Pr = 0.2$ $Ste = 0.02$ $V_{ref} = \frac{\nu_l}{H}$ |
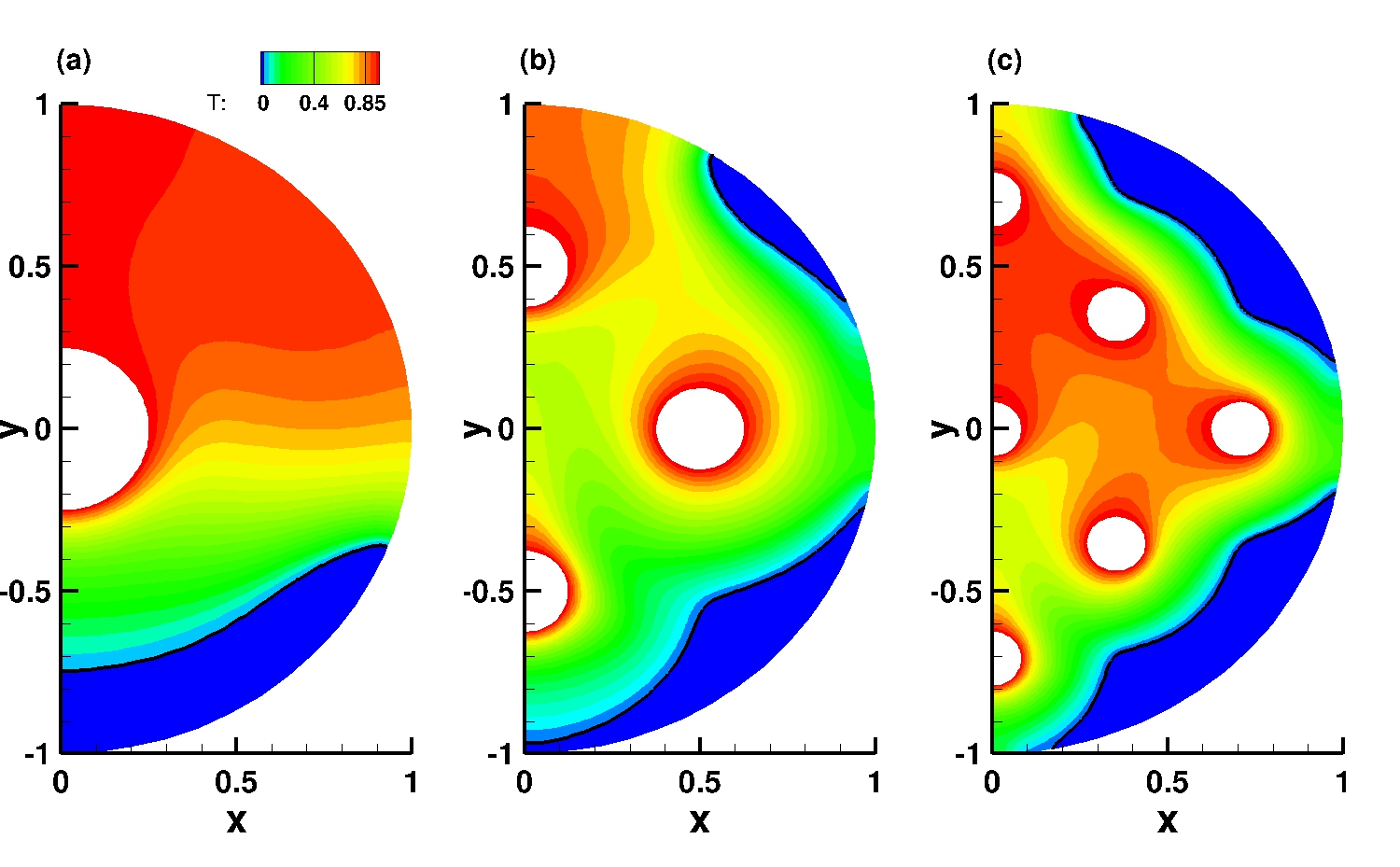
PCM Melting Case-3a: Melting of a circular PCM with one inner heated tube (Luo et al., 2015) ➟ Download/Watch movie |
 |
$Ra = 5 \cdot 10^4$ $Pr = 0.2$ $Ste = 0.02$ $V_{ref} = \frac{\nu_l}{H}$ |
PCM Melting Case-3b: Melting of a circular PCM with four inner heated tubes (Luo et al., 2015) ➟ Download/Watch movie |
 |
$Ra = 5 \cdot 10^4$ $Pr = 0.2$ $Ste = 0.02$ $V_{ref} = \frac{\nu_l}{H}$ |
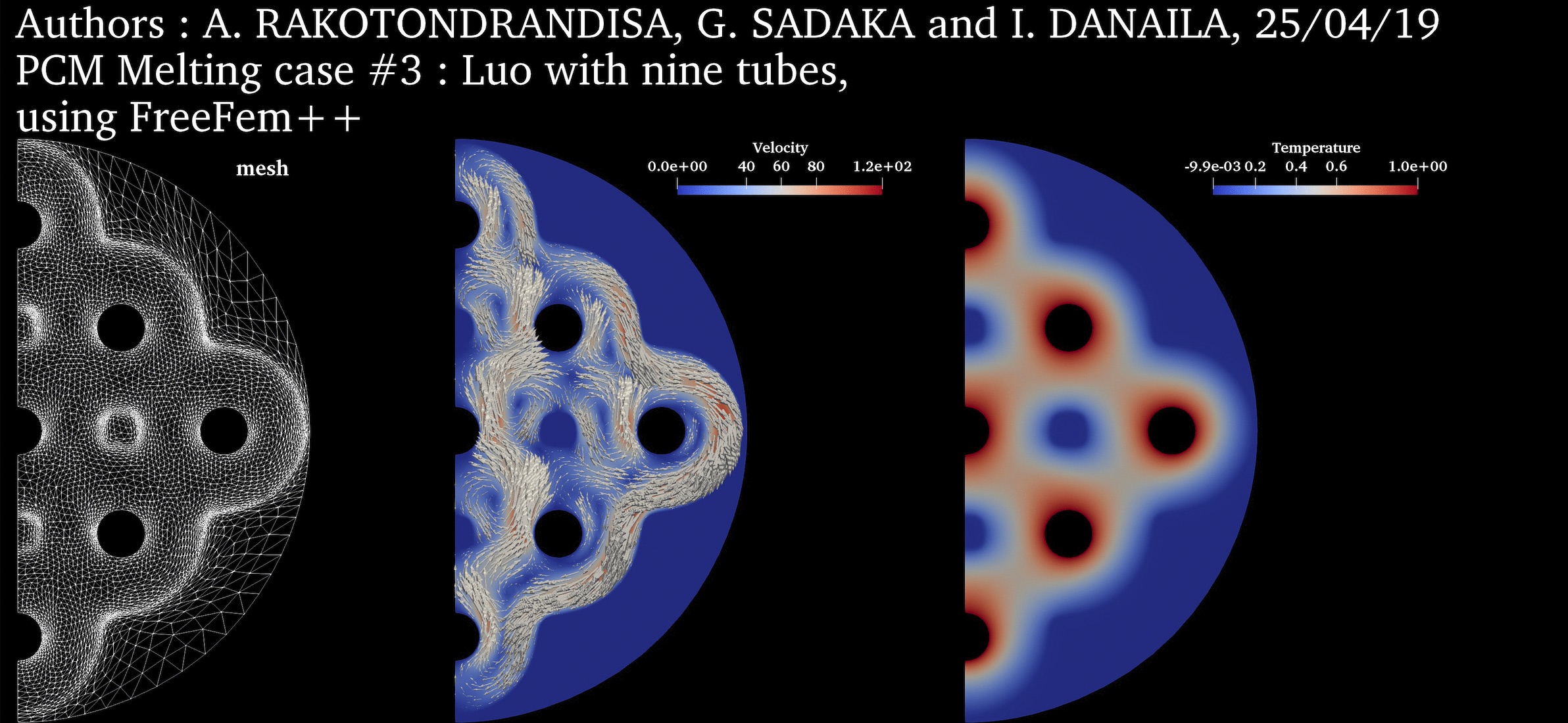
PCM Melting Case-3c: Melting of a circular PCM with nine inner heated tubes (Luo et al., 2015) ➟ Download/Watch movie |
 |
$Ra = 7 \cdot 10^5$ $Pr = 0.0216$ $Ste = 0.046$ $V_{ref} = \frac{\nu_l}{H}$ |
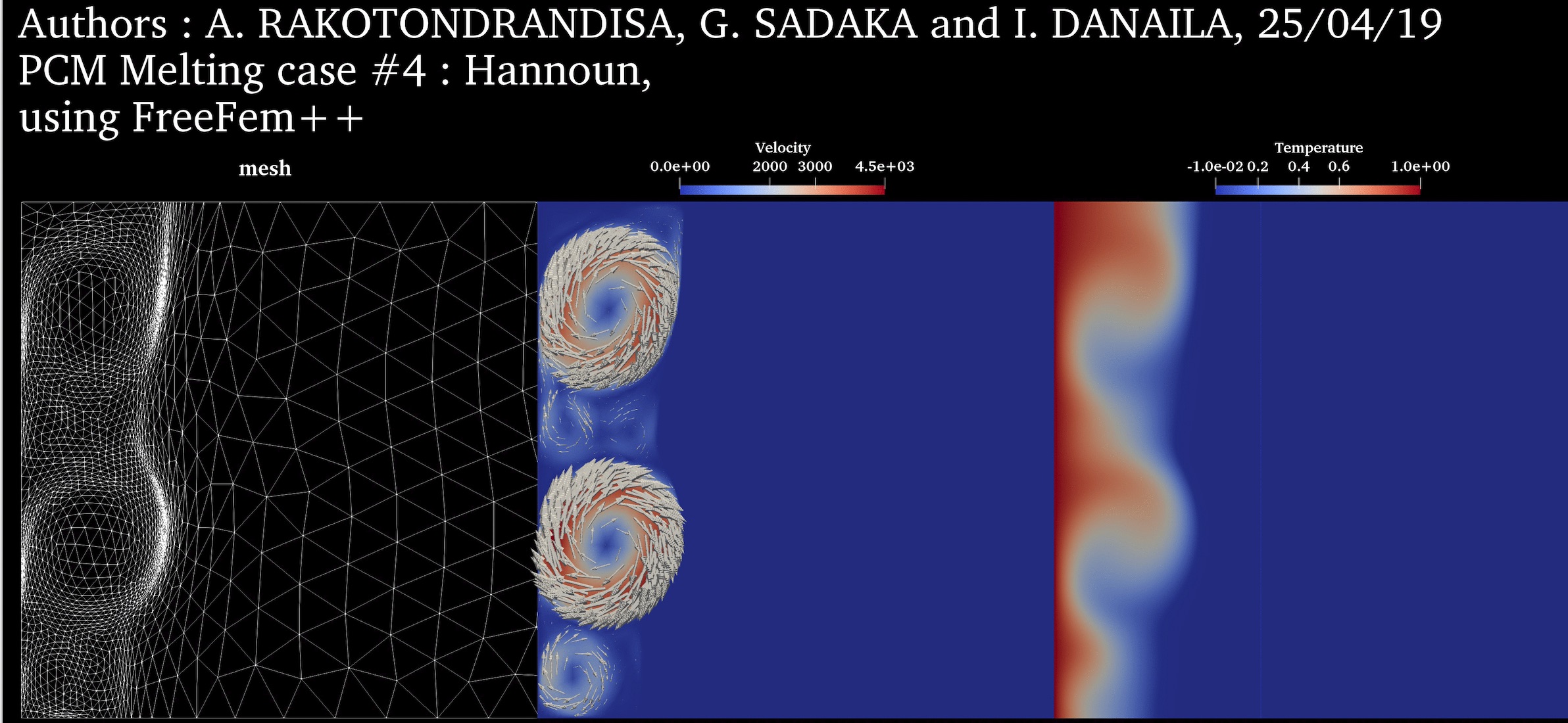
PCM Melting Case-4: Melting of Gallium in a rectangular cavity (Hannoun et al., 2003) ➟ Download/Watch movie |
 |
$Ra = 10^6$ $Pr = 0.1$ $Ste = 4.854$ $V_{ref} = \frac{\nu_l}{H} \sqrt{\frac{Ra}{Pr}}$ |
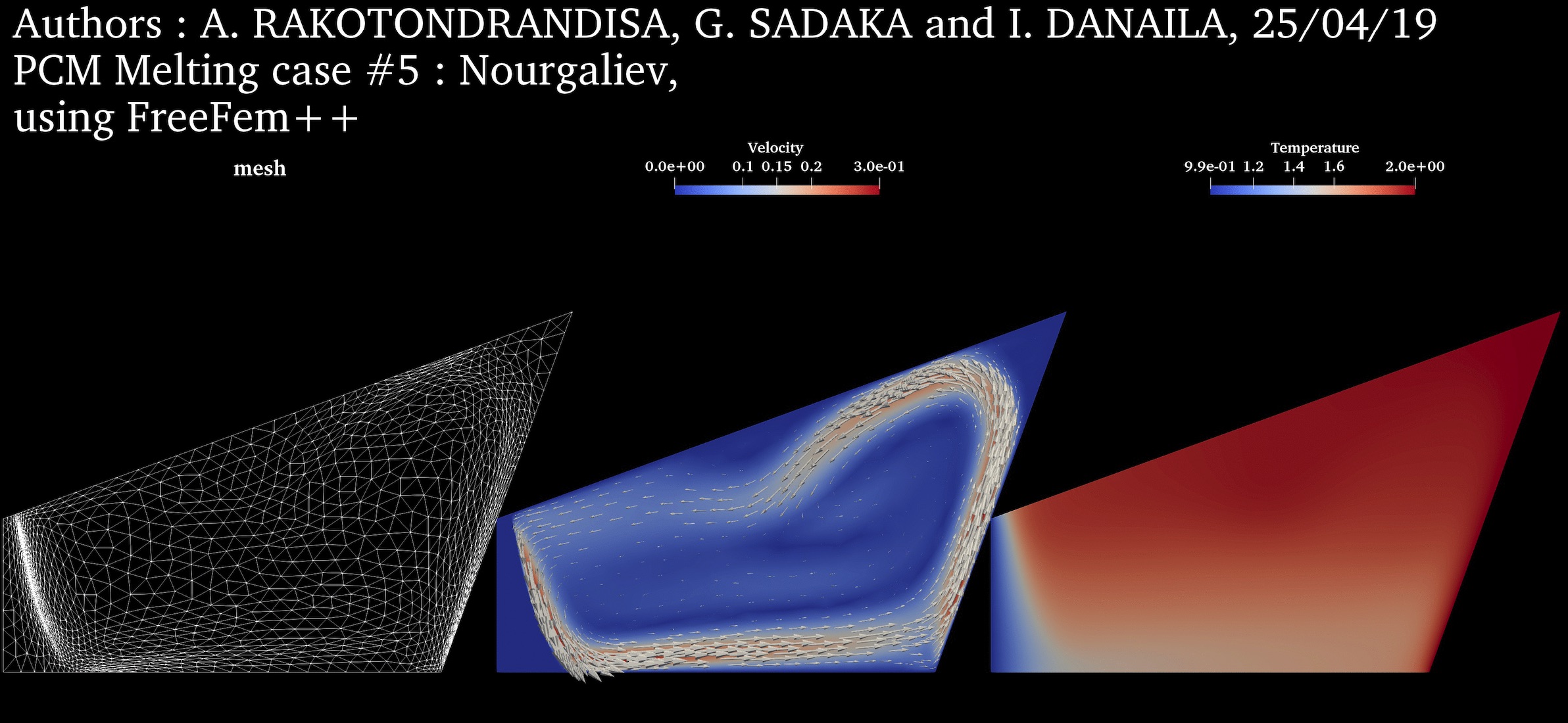
PCM Melting Case-5: Solid crust formation in a highly distorted PCM (Nourgaliev et al., 2015) ➟ Download/Watch movie |
 |
$Ra = 3.27 \cdot 10^5$ $Pr = 56.2$ $Ste = 0.045$ |
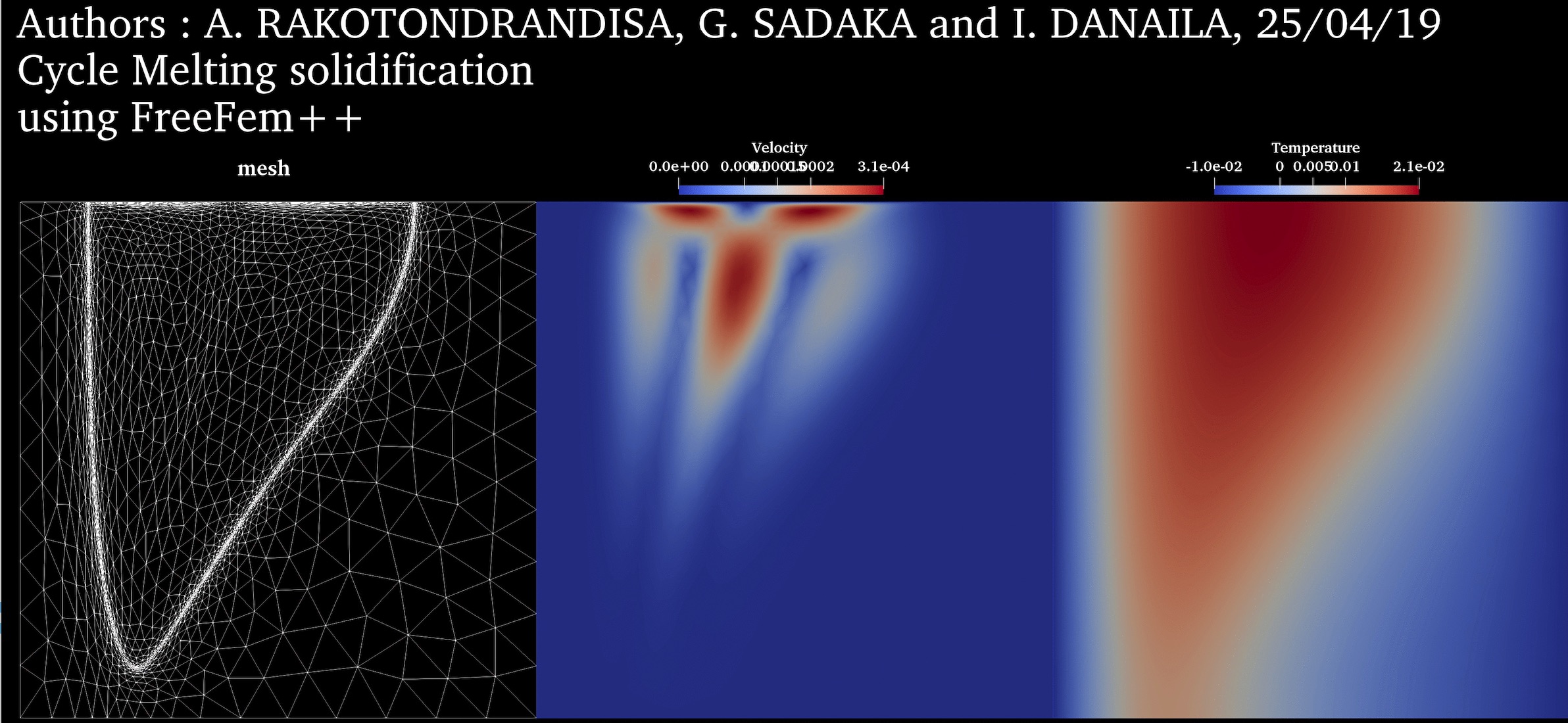
Melting-solidification cycle: PCM Melting-1 (Okada, 1994) followed by the solidification from the left boundary. ➟ Download/Watch movie |
 |
$T_{left} = 10 ^oC$ (natural convection) $T_{right}= 0 ^oC$ (natural convection) $T_{left} = 10 ^oC$ (freezing) $T_{right}=-10 ^oC$ (freezing) |
Water freezing: the natural concetion state is first computed and then used as initial condition for simulating the freezing process. ➟ Download/Watch movie |
