Download preprint-pdf

Authors

G. Sadaka, V. Kalt, I. Danaila and F. Hecht

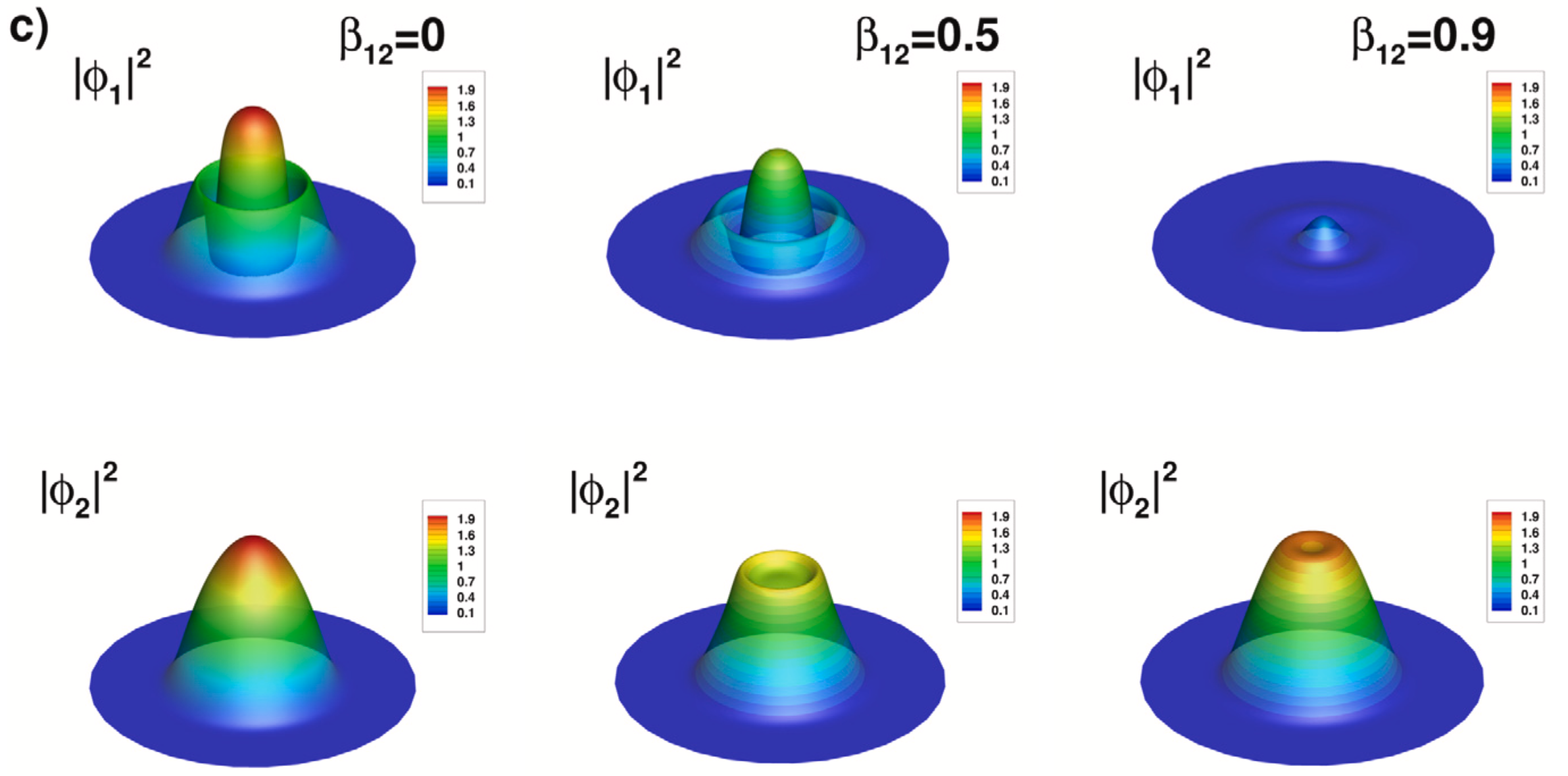
Abstract

We present a finite element toolbox for the computation of Bogoliubov-de Gennes modes used to assess the linear stability of stationary solutions of the Gross-Pitaevskii (GP) equation. Applications concern one (single GP equation) or two-component (a system of coupled GP equations) Bose-Einstein condensates in one, two and three dimensions of space. An implementation using the free software \ff is distributed with this paper. For the computation of the GP stationary (complex or real) solutions we use a Newton algorithm coupled with a continuation method exploring the parameter space (the chemical potential or the interaction constant). Bogoliubov-de Gennes equations are then solved using dedicated libraries for the associated eigenvalue problem. Mesh adaptivity is proved to considerably reduce the computational time for cases implying complex vortex states. Programs are validated through comparisons with known theoretical results for simple cases and numerical results reported in the literature.

Supplemental material: 2D centered dark soliton case

Snapshots of the solution for $\mu=3$	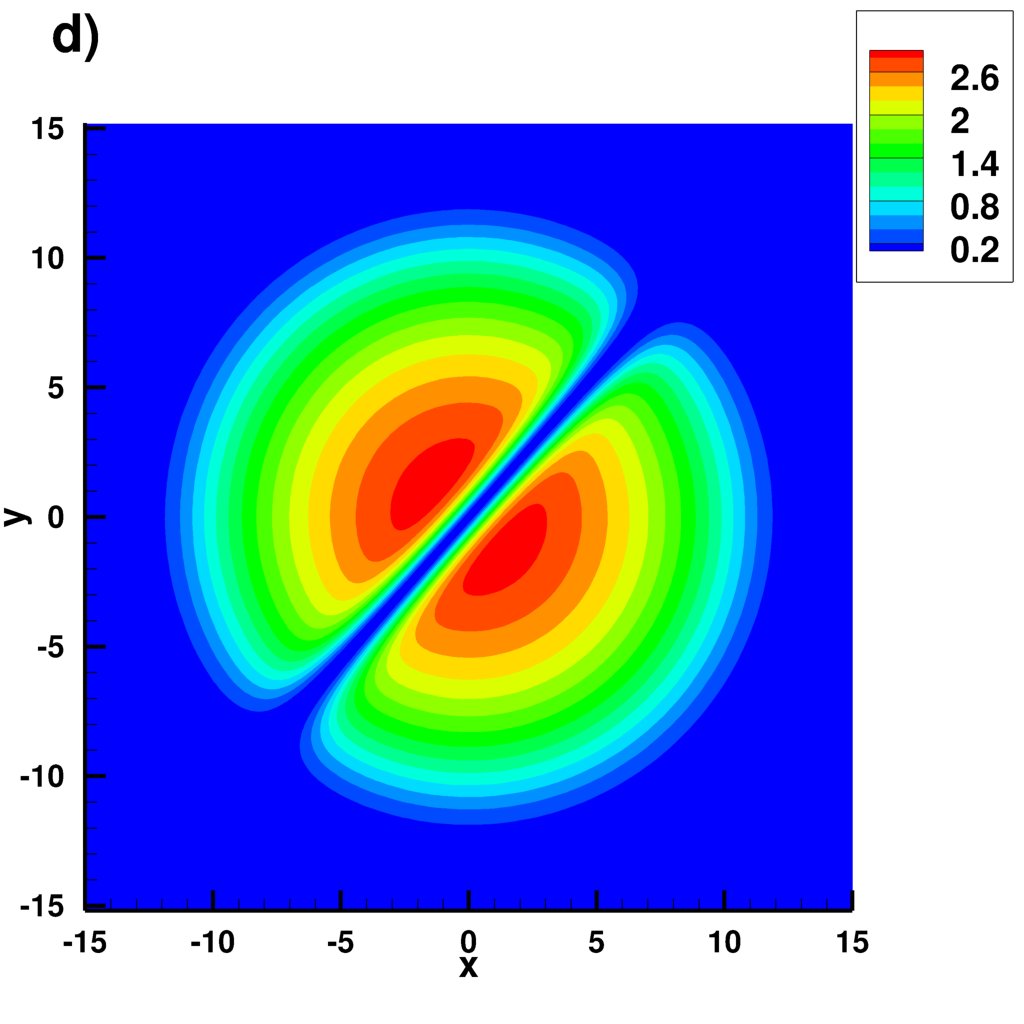Real part $\omega_r$ of eigenvalues	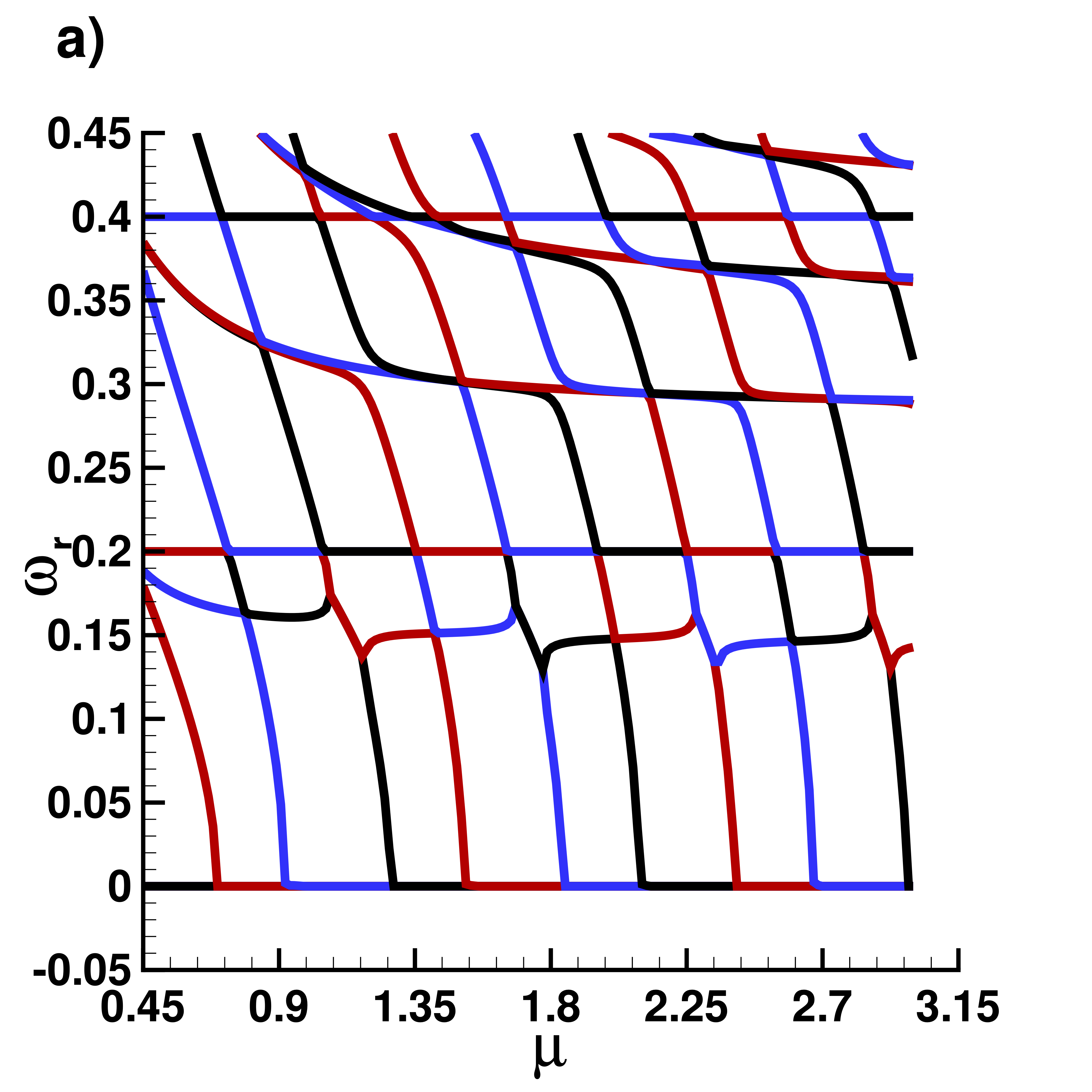Imaginary part $\omega_i$ of eigenvalues

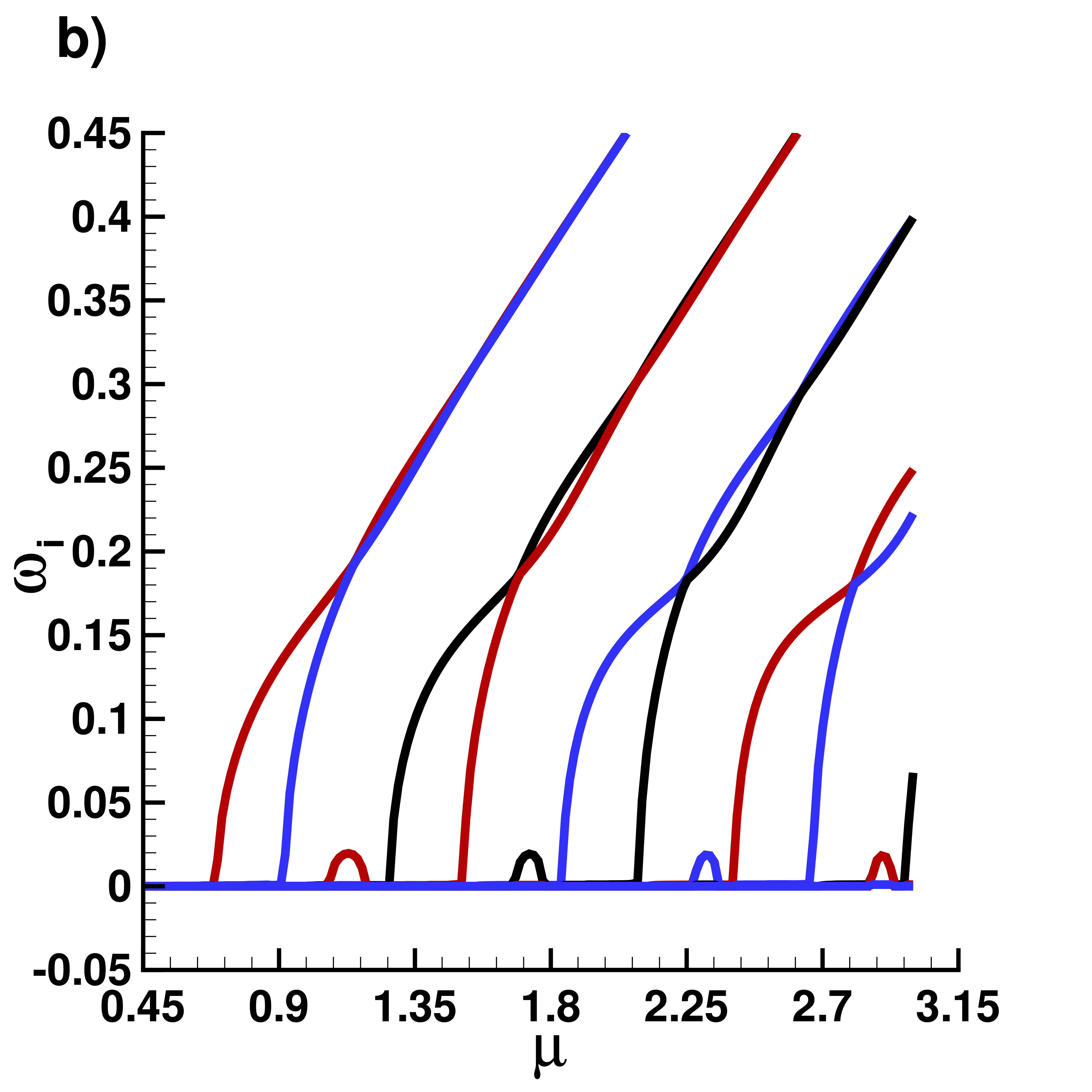Supplemental material: 2D central vortex case

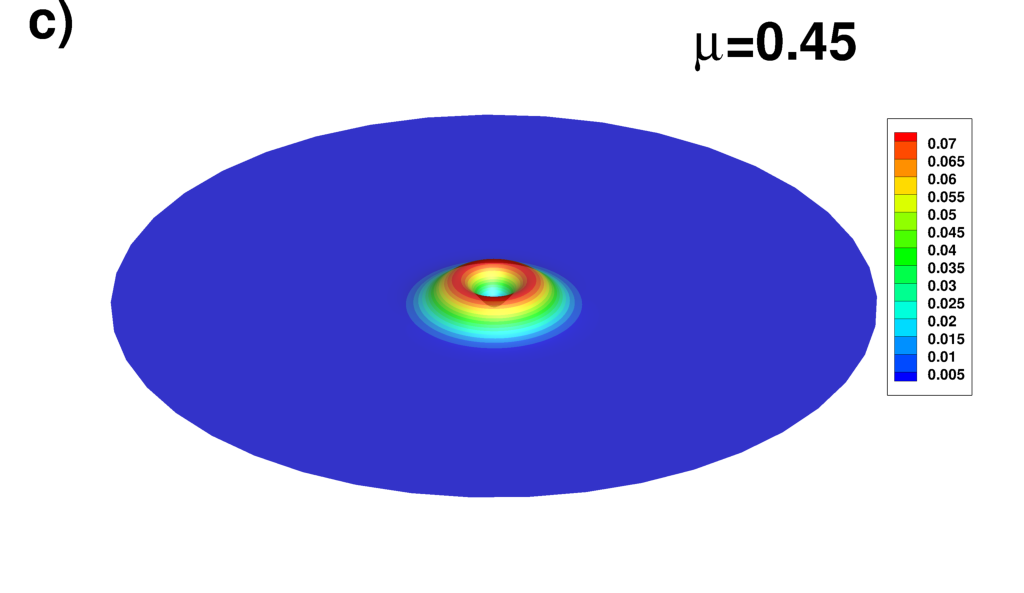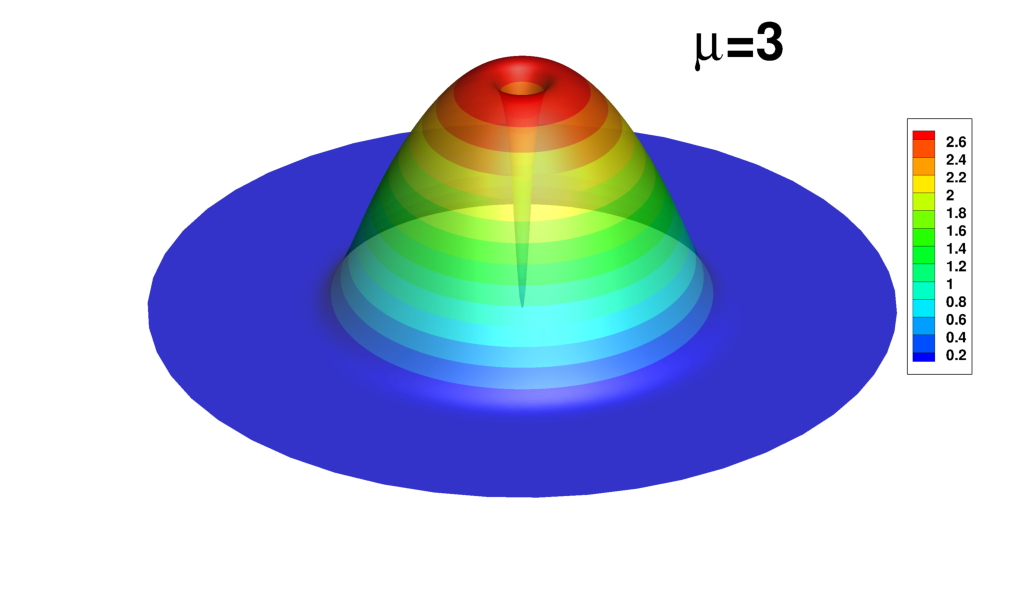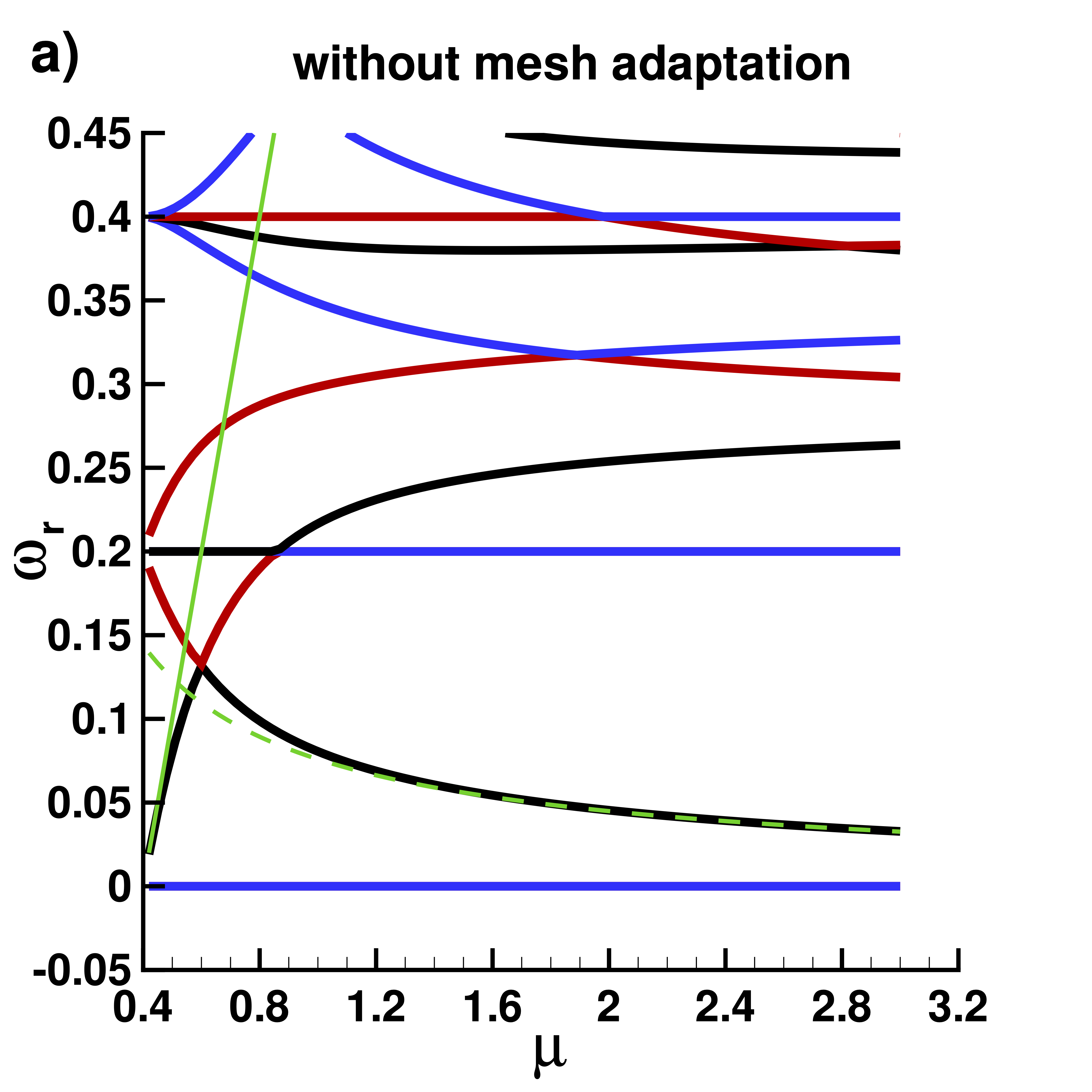
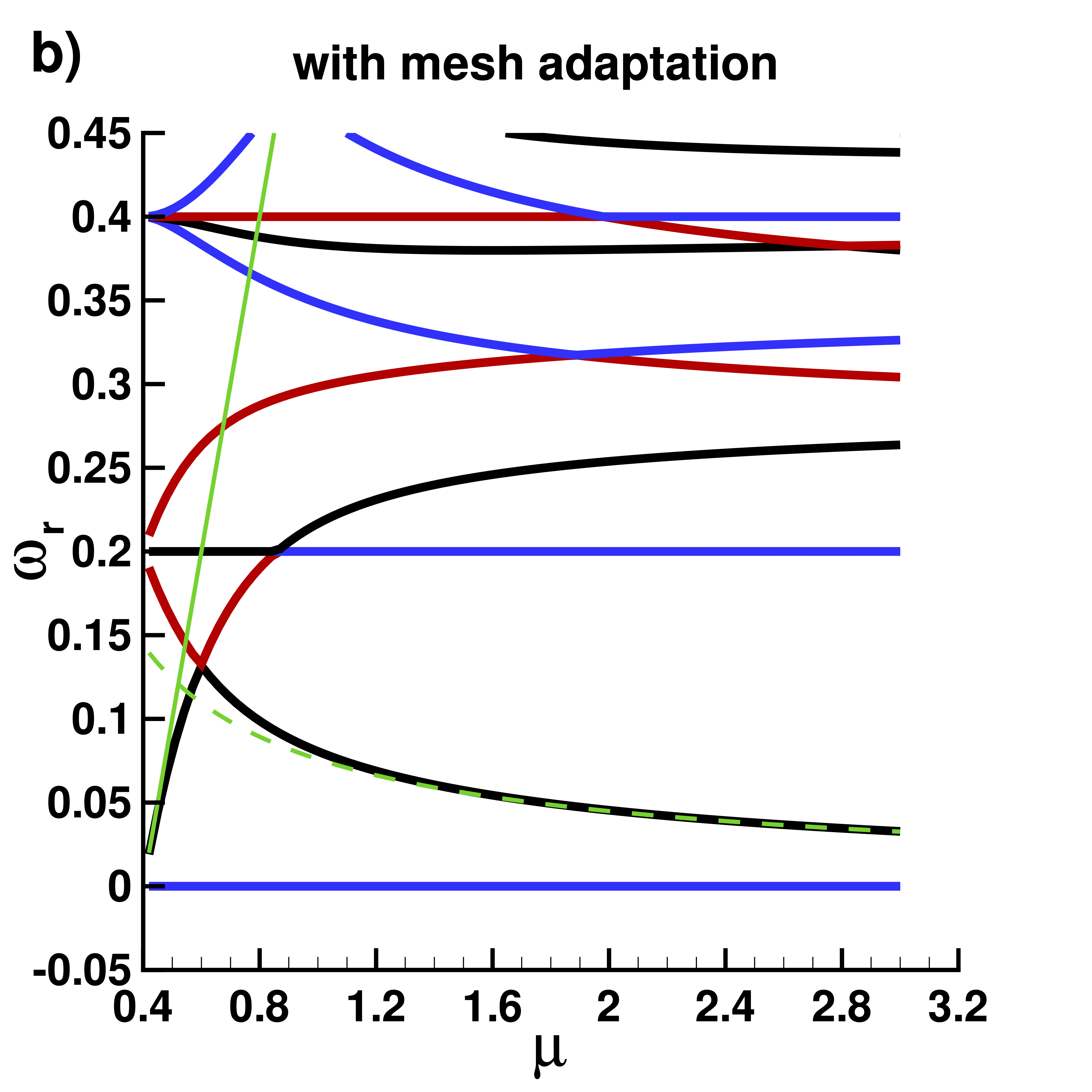
Snapshots of the solution	Real part $\omega_r$ of eigenvalues without mesh adaptation	Real part $\omega_r$ of eigenvalues with mesh adaptation

Supplemental material: 2D ring-antidark-ring state case

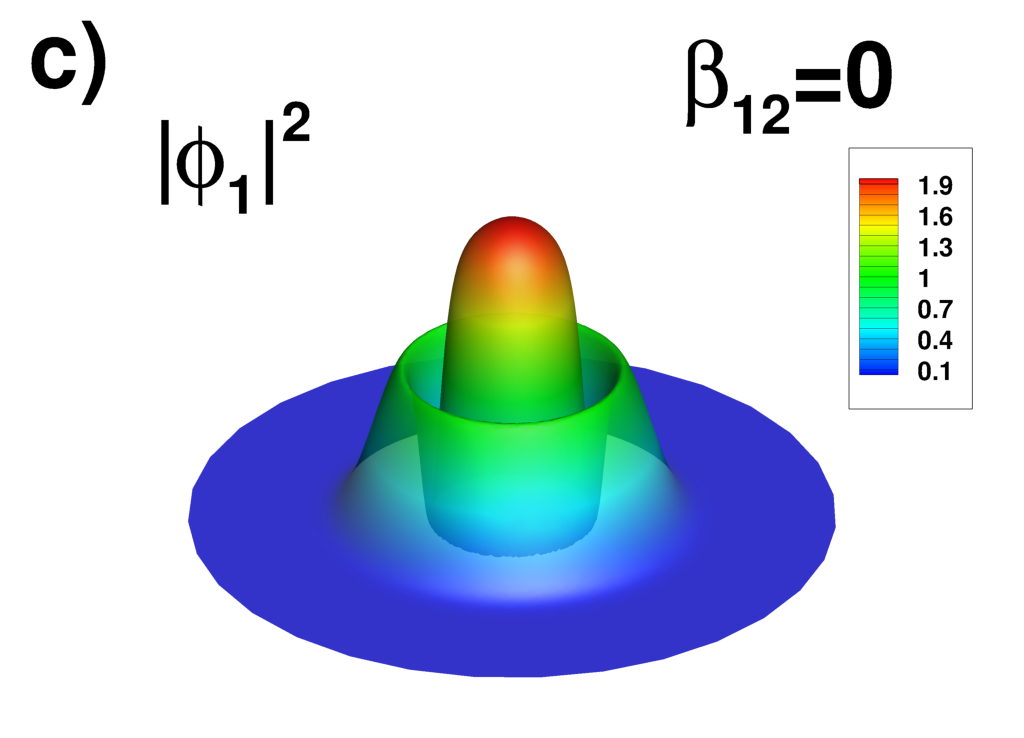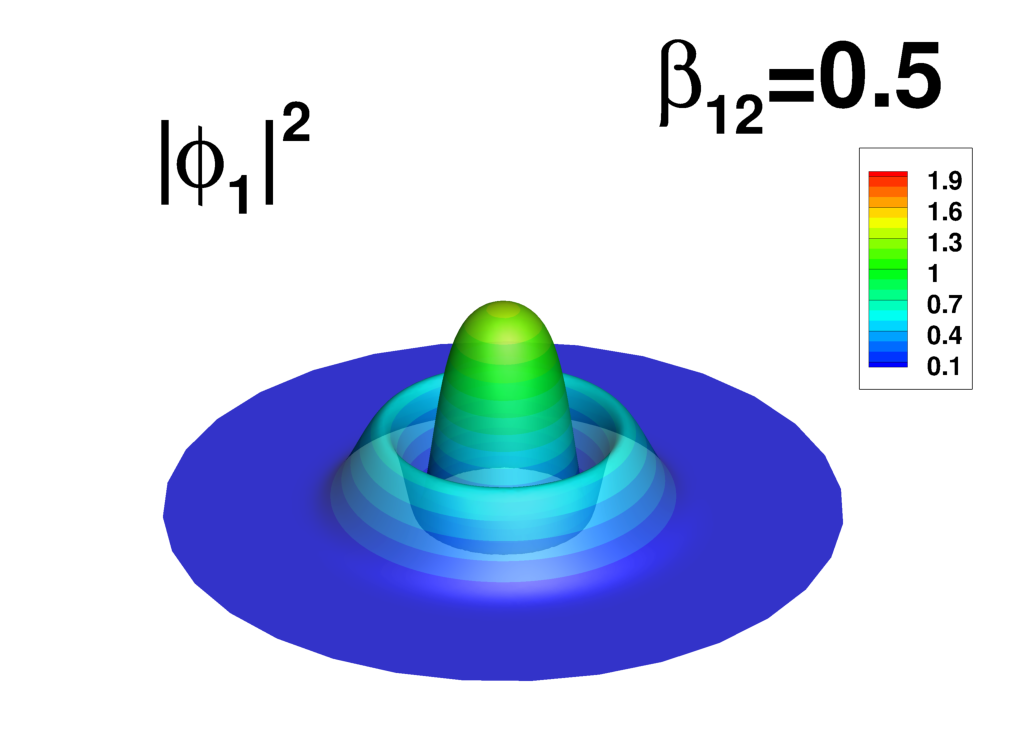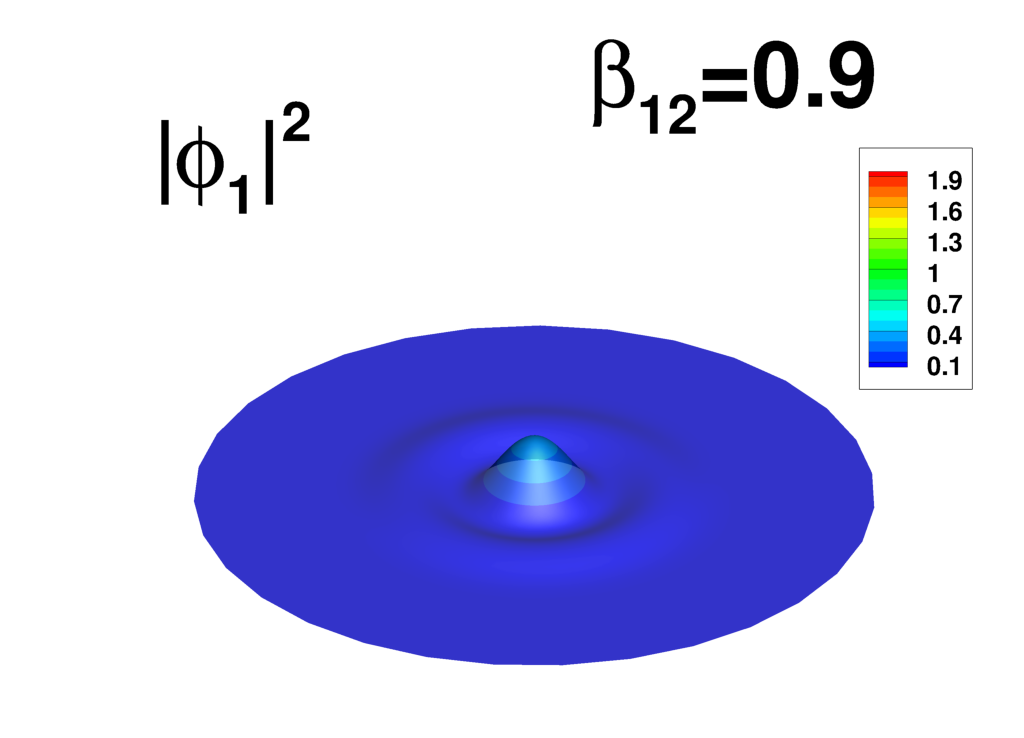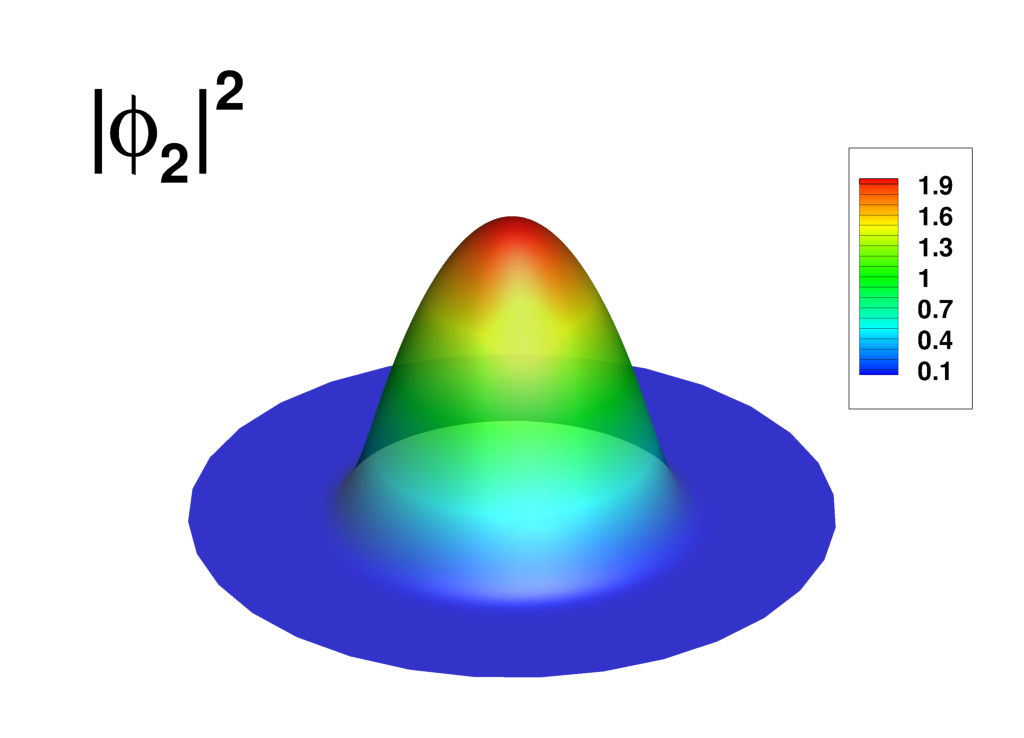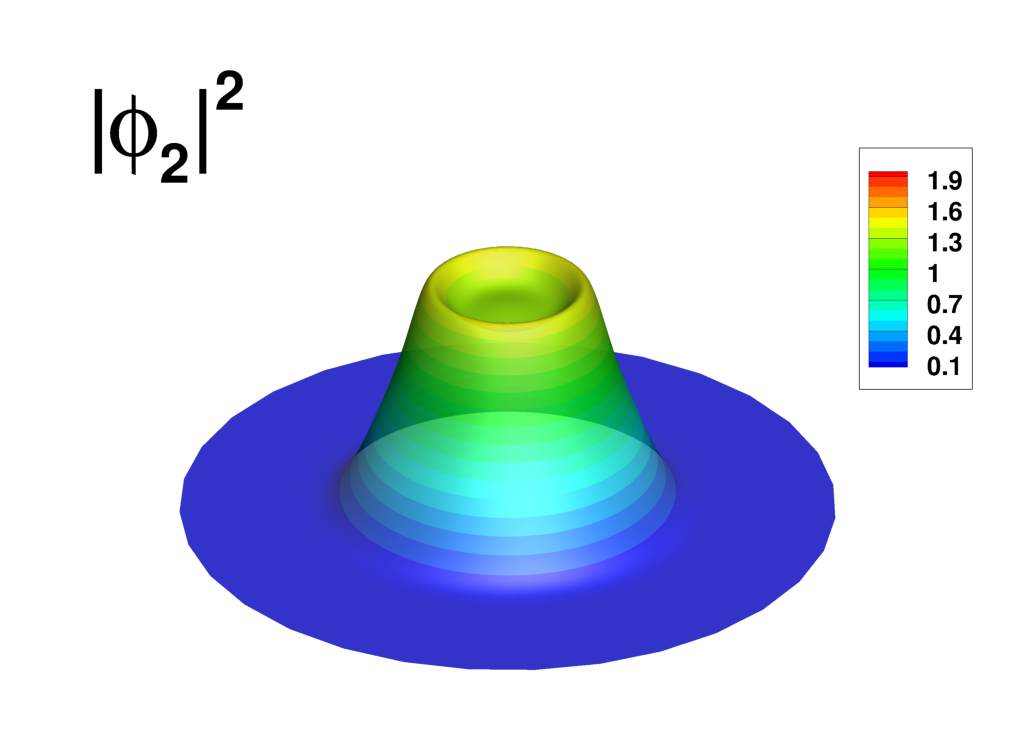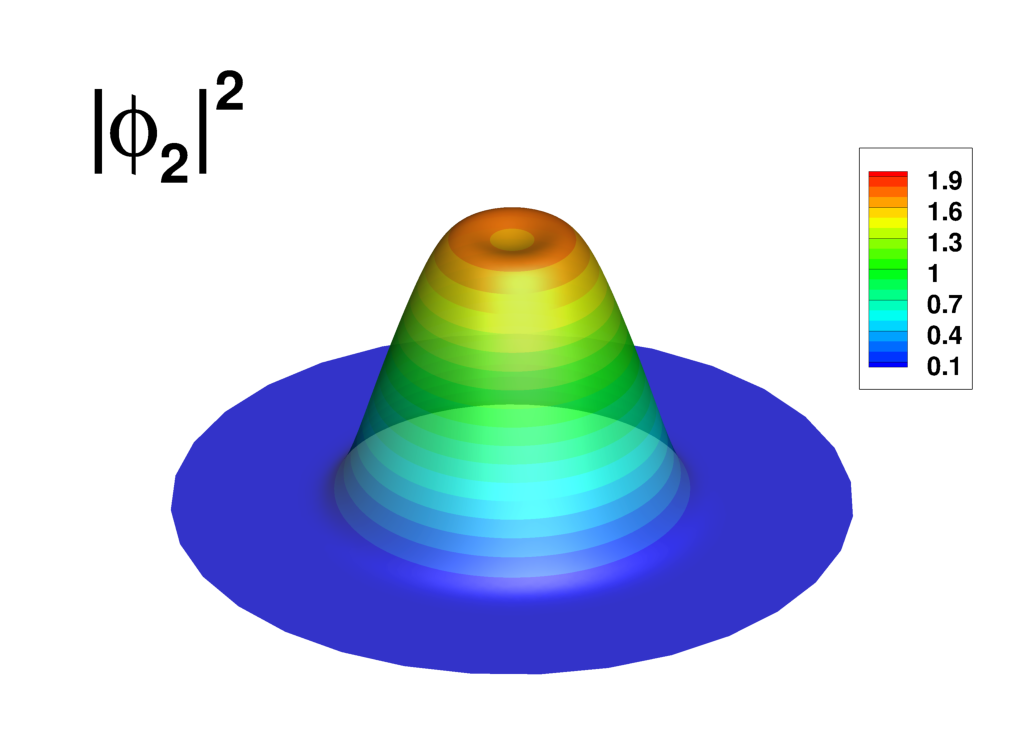Real part $\omega_r$ of eigenvalues	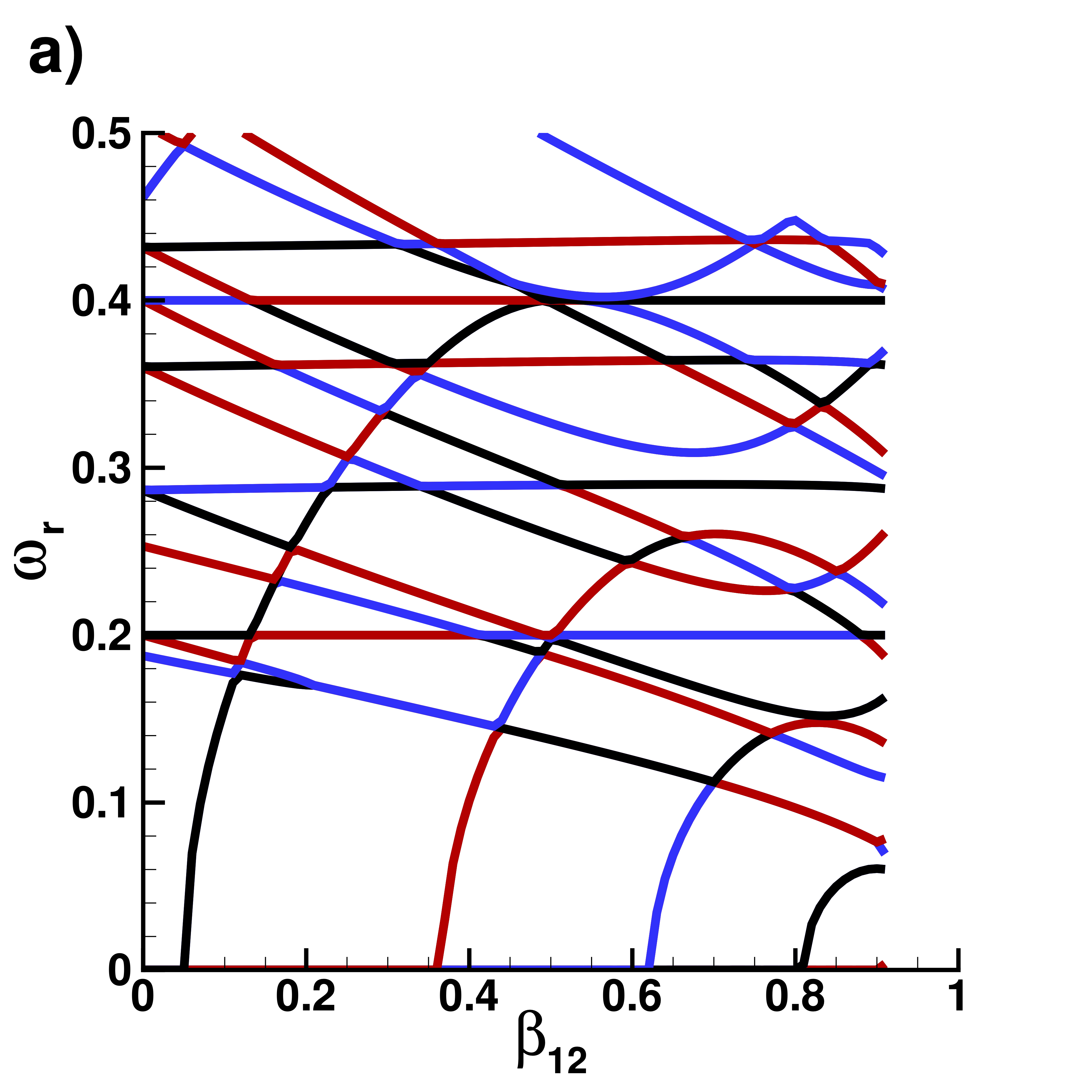Imaginary part $\omega_i$ of eigenvalues

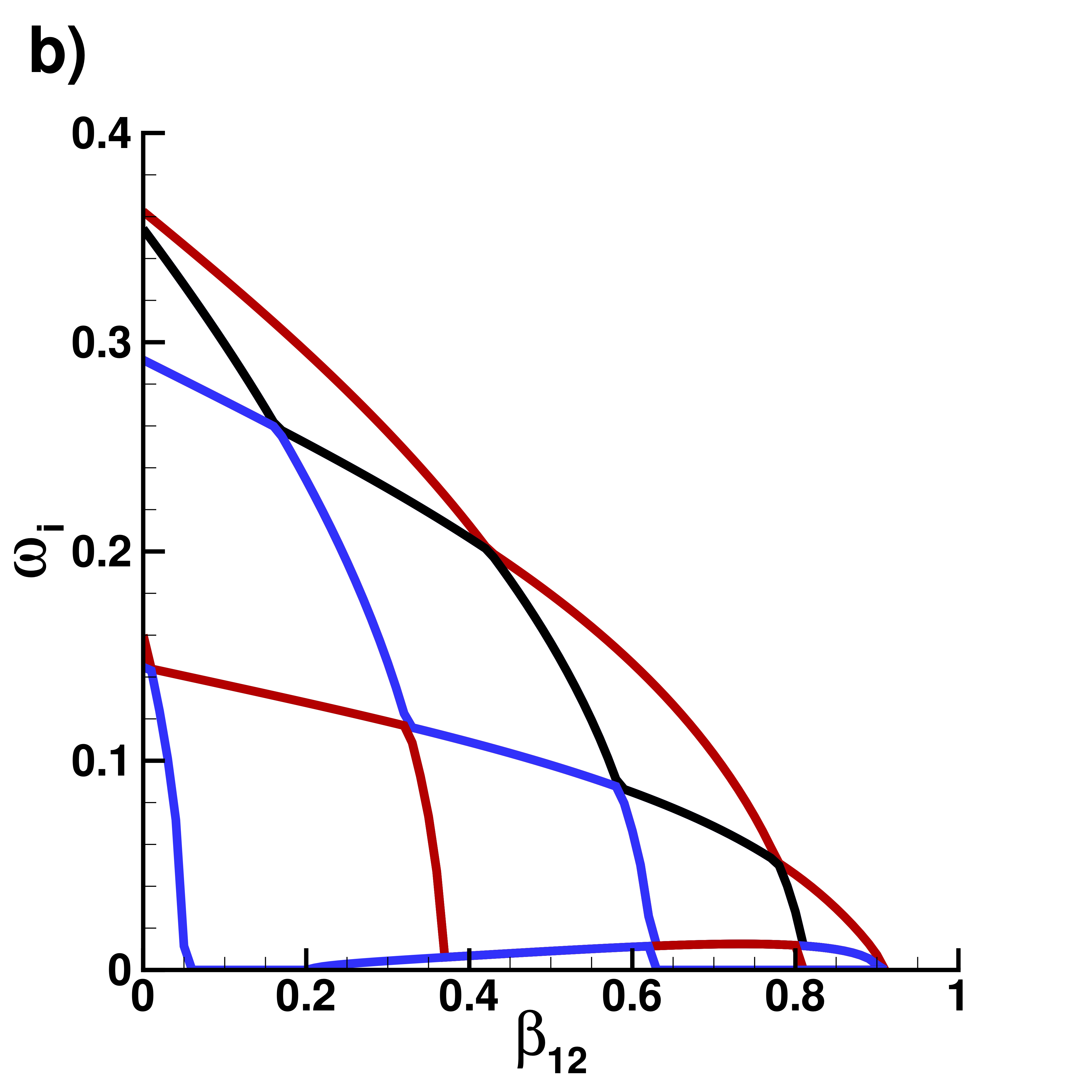Supplemental material: 3D ground state case

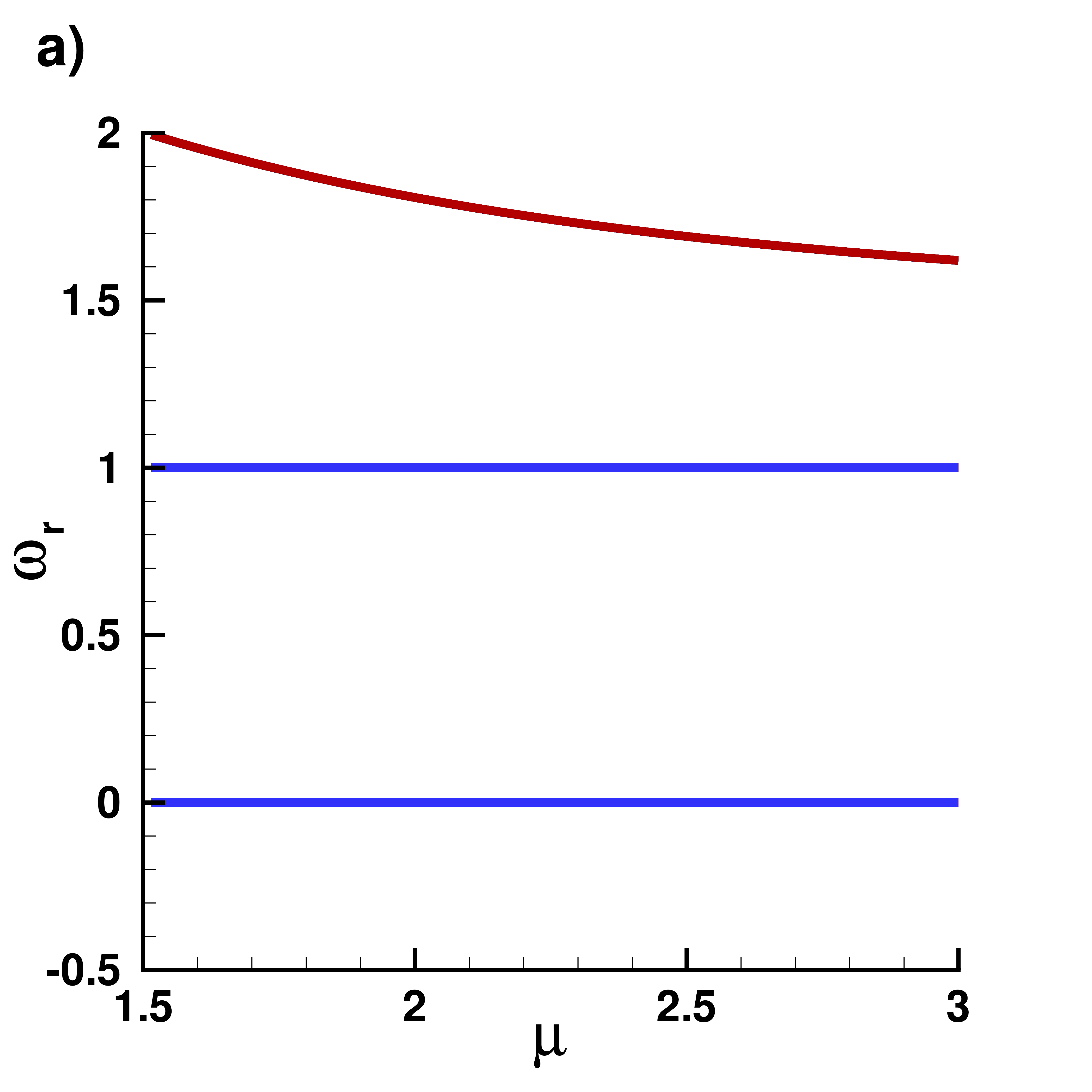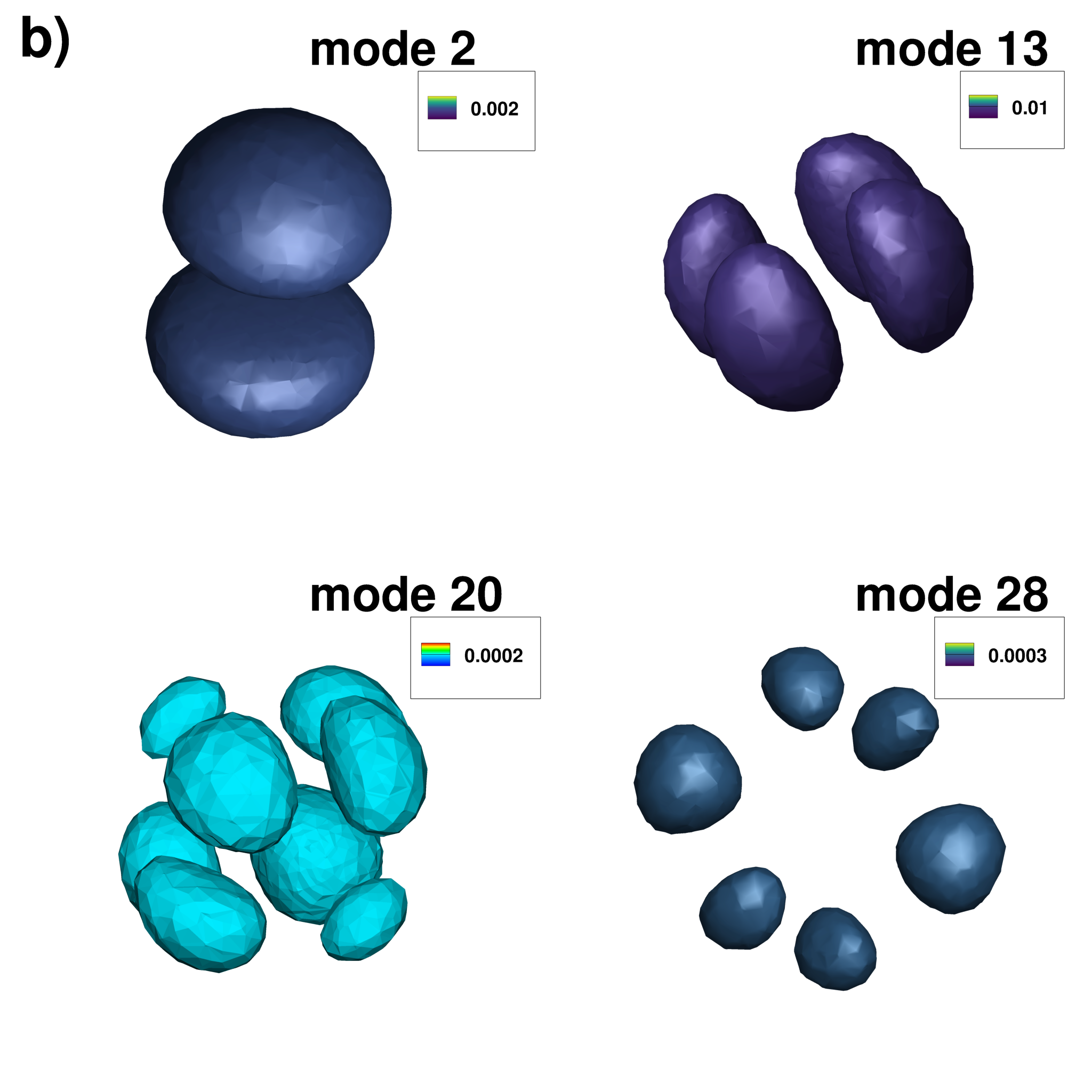
Real part $\omega_r$ of eigenvalues	Illustration of four BdG modes (iso-surfaces of the modulus)