Authors
G. Edde, G. Sadaka, R. Antoine and I. Danaila
Abstract
We present two- and three-dimensional numerical simulations of the natural convection flow within an artificial underground cavity. We consider a realistic geometry reconstructed from measurements (3D point cloud obtained with a photogrammetric method) of the Barcq cavity existing in Normandy region, France. The numerical model solves the Navier-Stokes equations coupled with the unsteady heat equation using a finite-element method for the space discretization. Time integration is based on a semi-implicit method and the Newton method to solve the resulting non-linear equation. To implement the method, we use the free software FreeFem++ offering efficient mesh refinement/adaptivity tools. The parallelization of the simulations relies upon the PETSc software library, to which FreeFem++ offers an easy-to-use interface. We analyze the onset of the natural convection and characterize the convective cells developing within the Barcq cavity for four Rayleigh (Ra) numbers (from $10^{5}$ to $10^{8}$). Dimensionless temperatures, velocities and Nusselt numbers are presented for each Ra number. We discuss how these results can be used to understand the thermal behavior of small artificial cavities. We address in particular the influence of the value of the Rayleigh number on the flow inside the well, which is essential for designing detection methods based on surface temperature observations.
FreeFem++ Code
Source code
Supplemental material: mesh generation
|
|
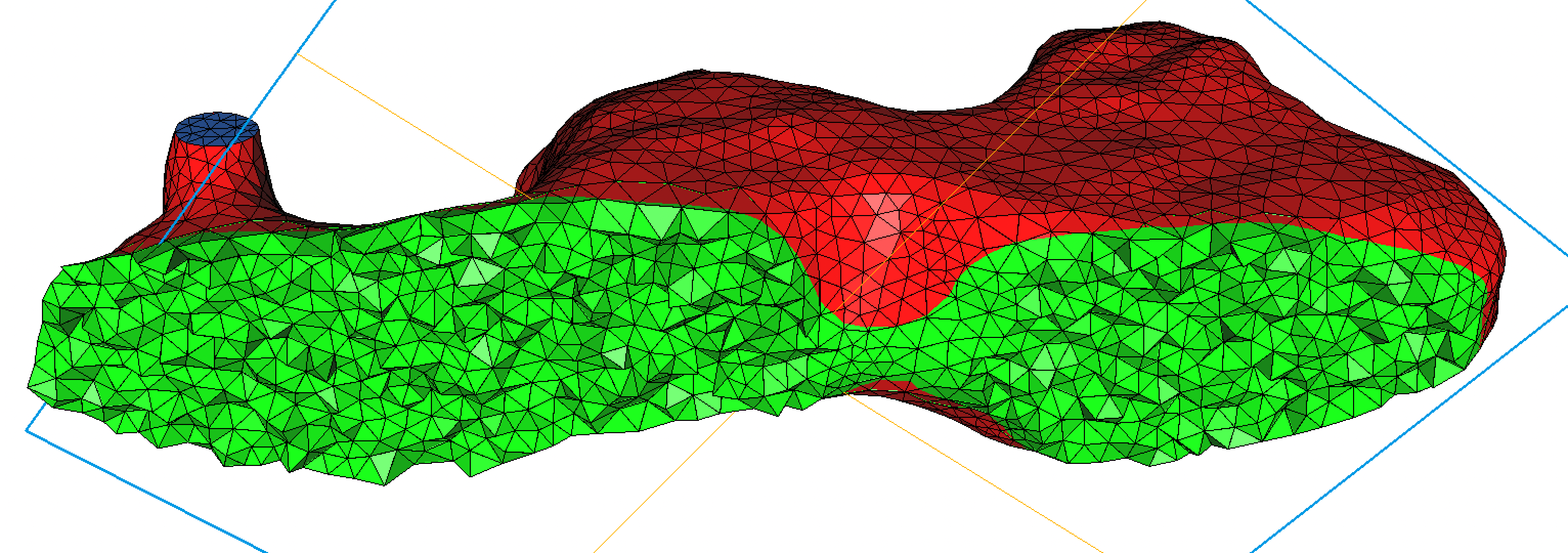
Full 3D mesh (tetrahedra) generated using the 3D-points cloud from photogrammetric measurements
|
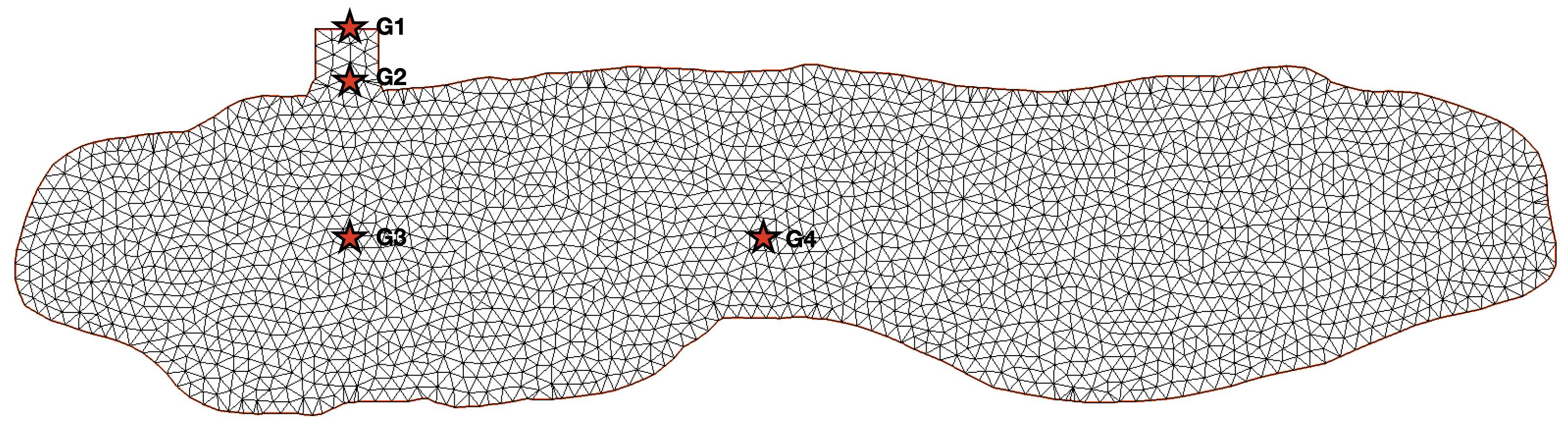
2D mesh (triangles) is the graphical parallel projection of the 3D mesh on the meridian plane. Gauges G1, G2, G3 and G4 are also represented
|
Supplemental material: snapshots of the natural convection flow for different values of the Rayleigh number
Results for the 2D configuration
Velocity vectors and contours of the velocity magnitude (colors)
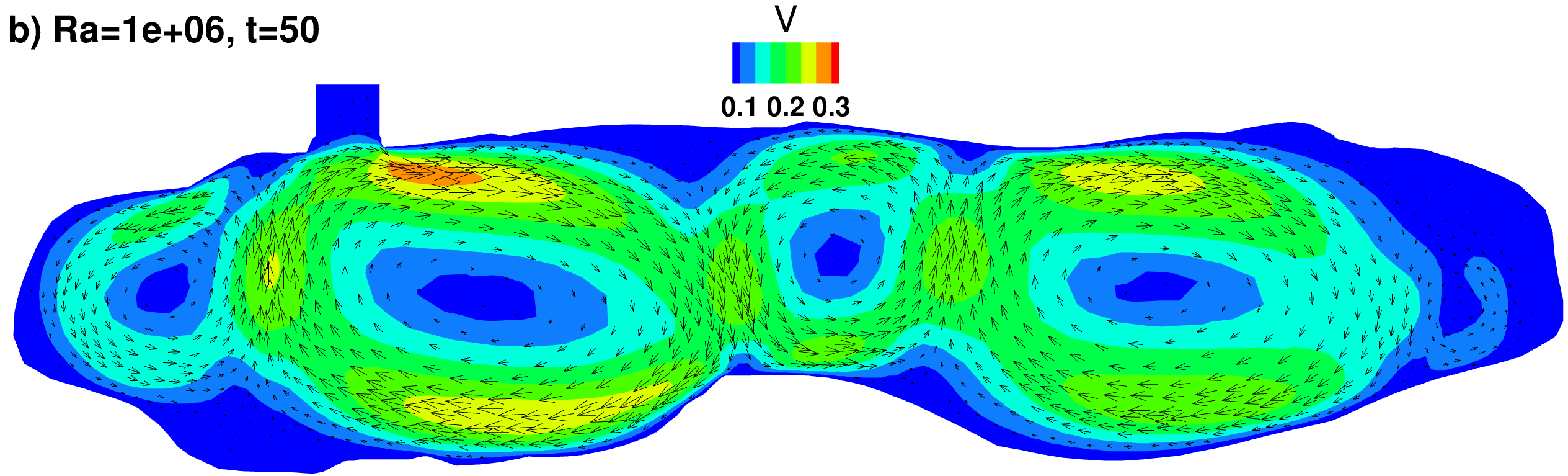 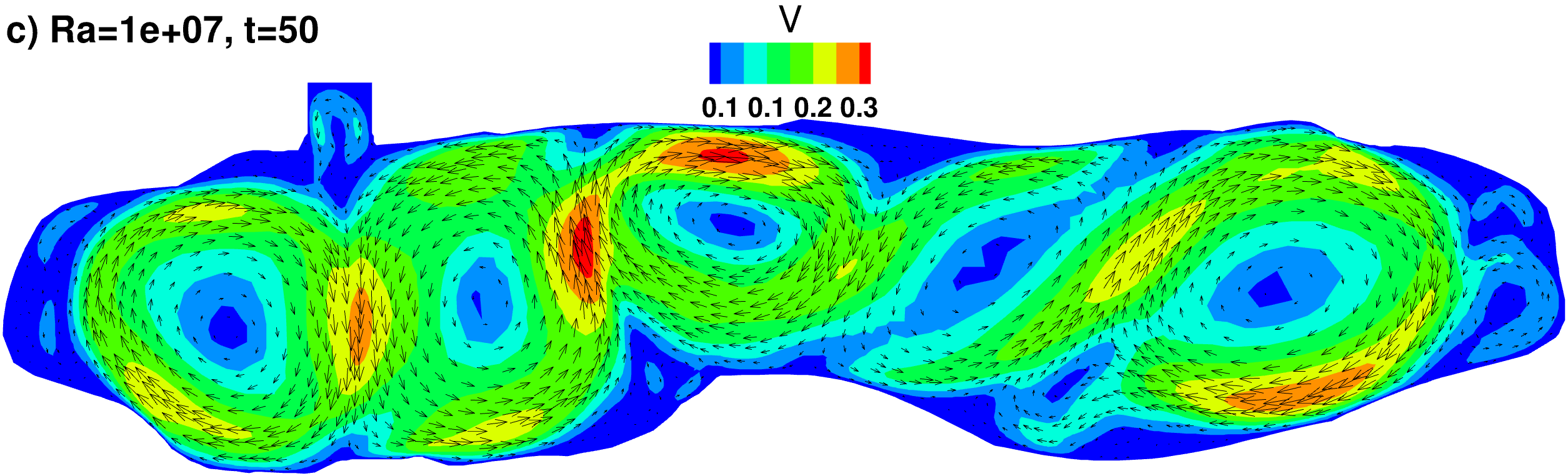 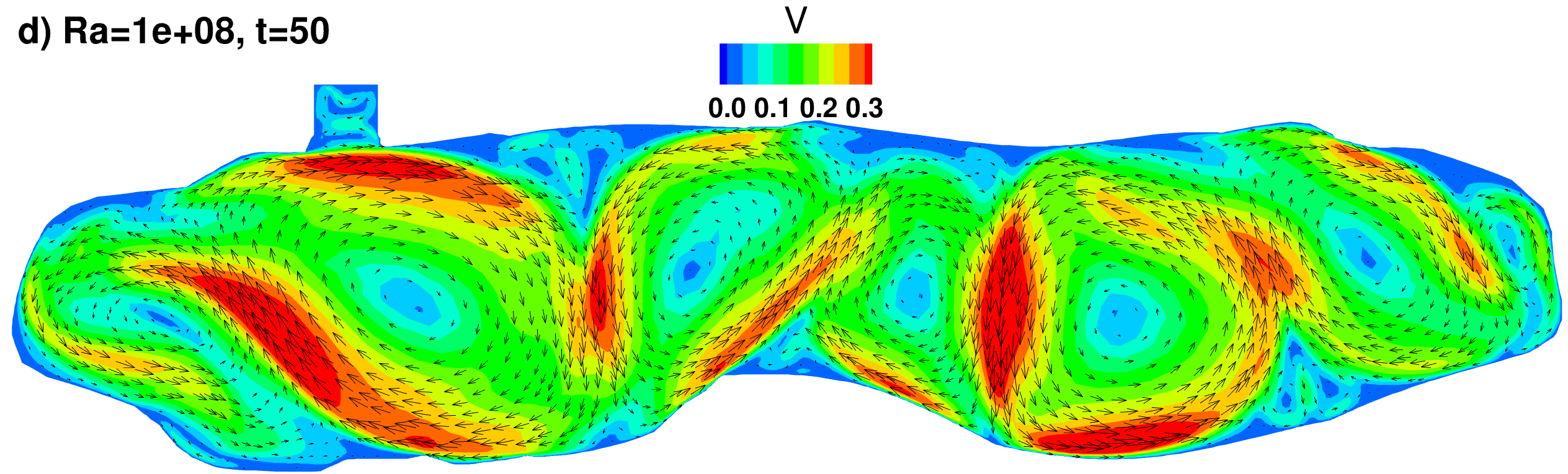 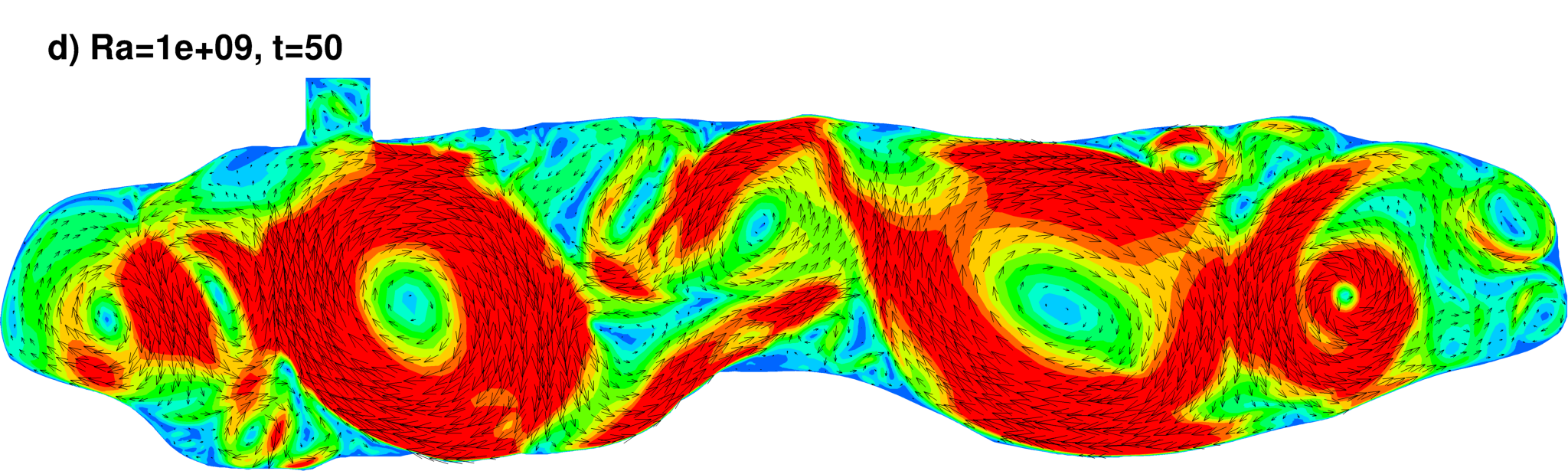
|
Temperature contours
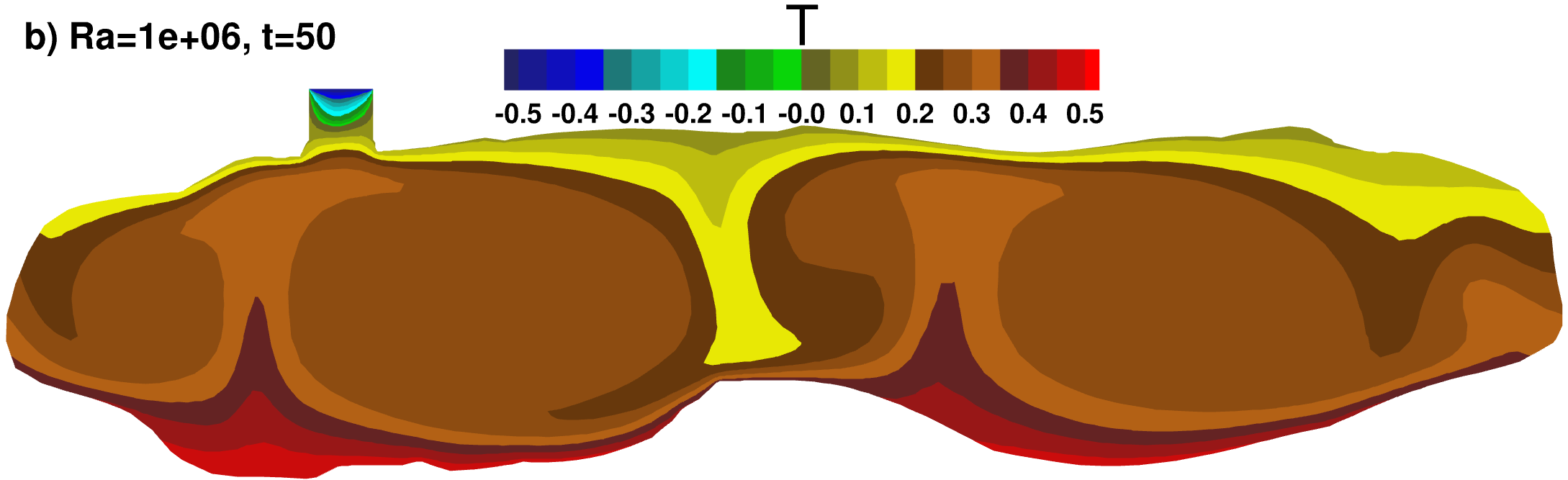 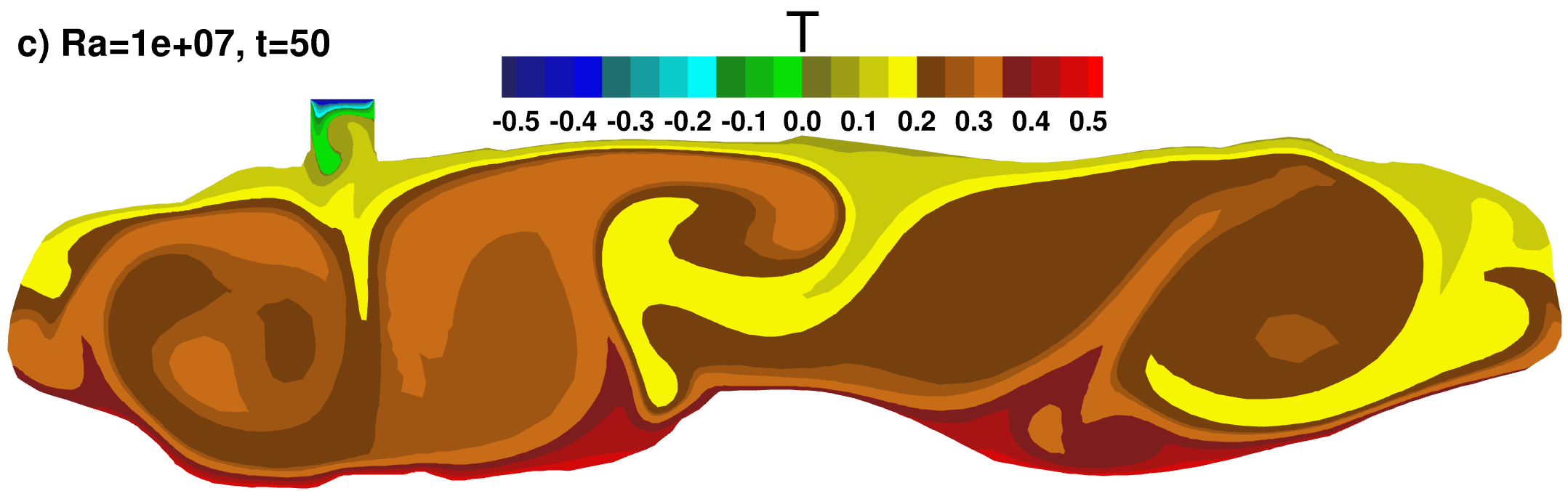 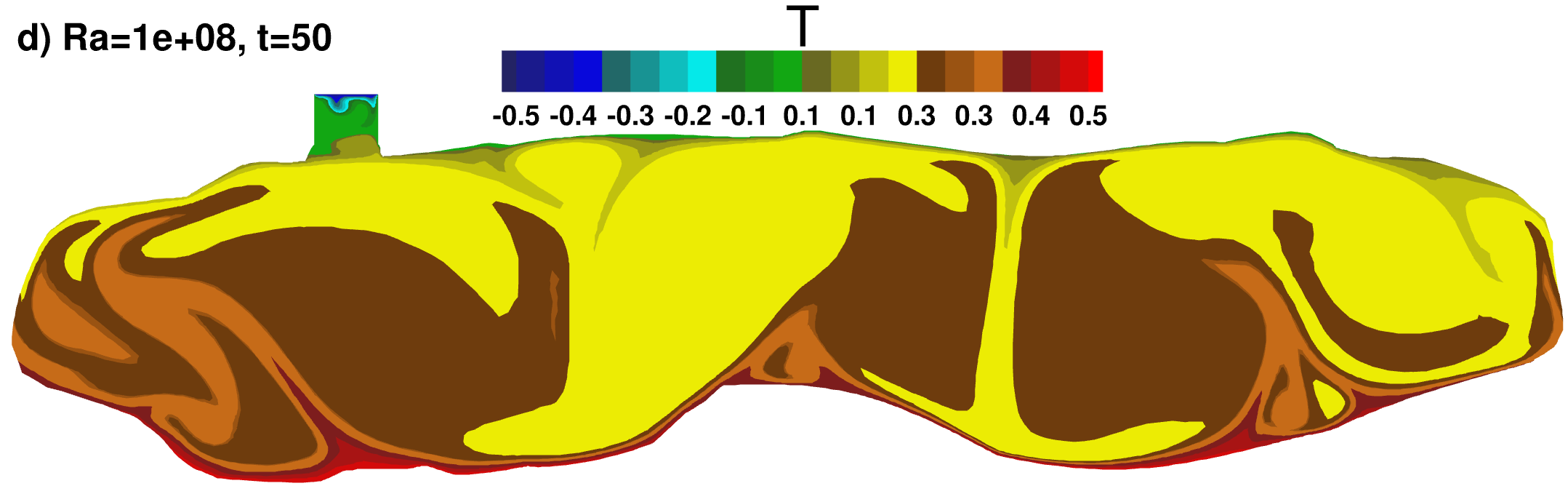 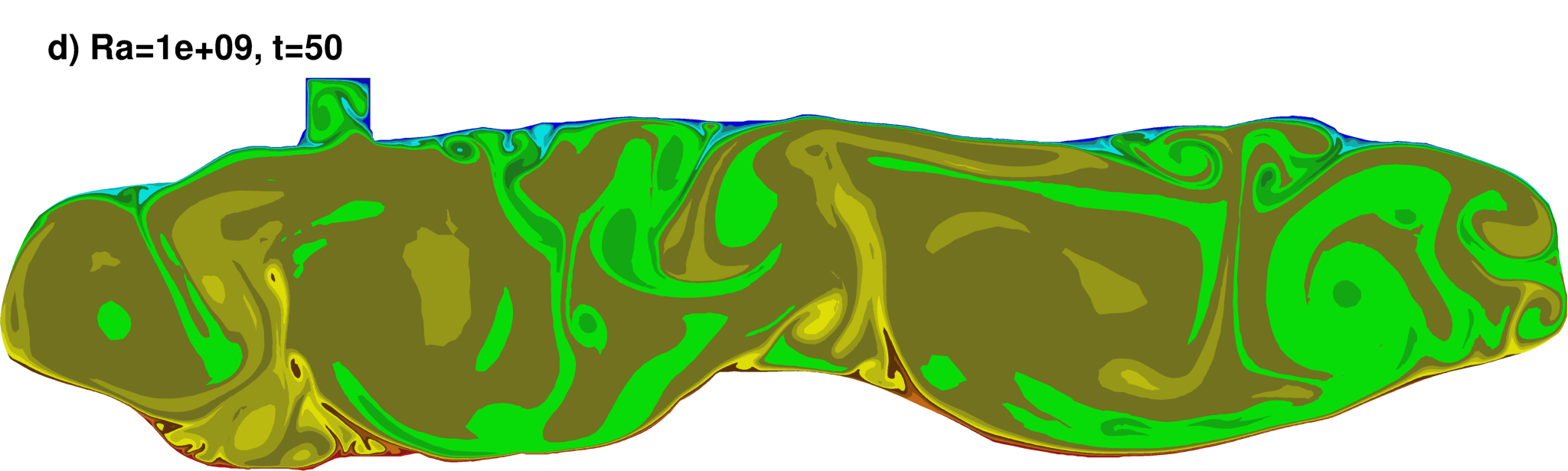
|
Adapted finite element mesh
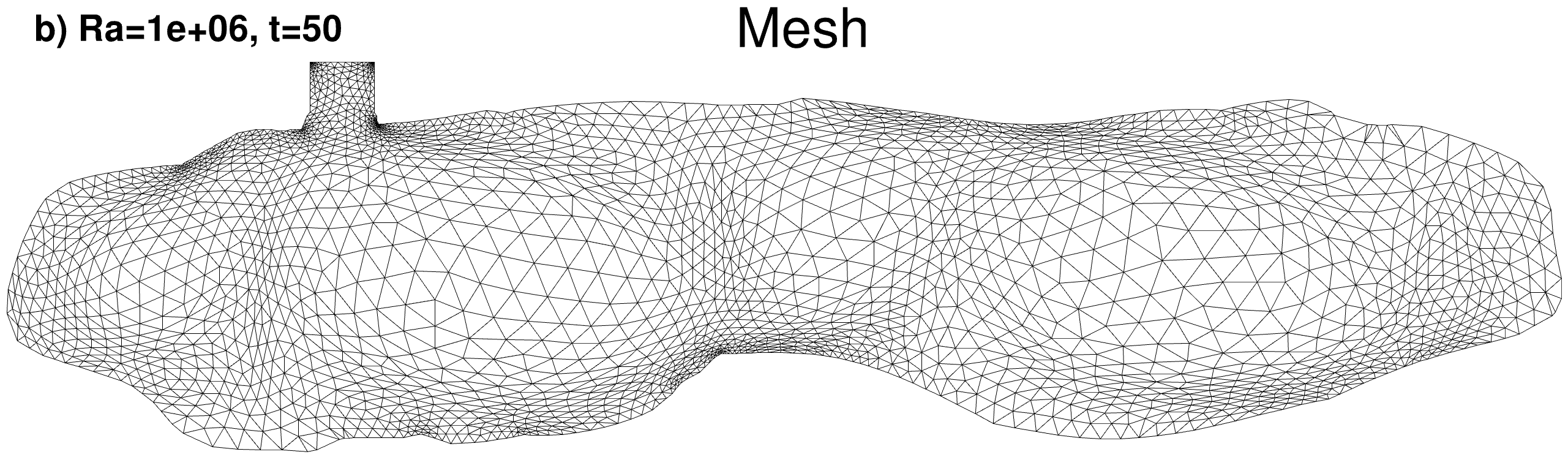 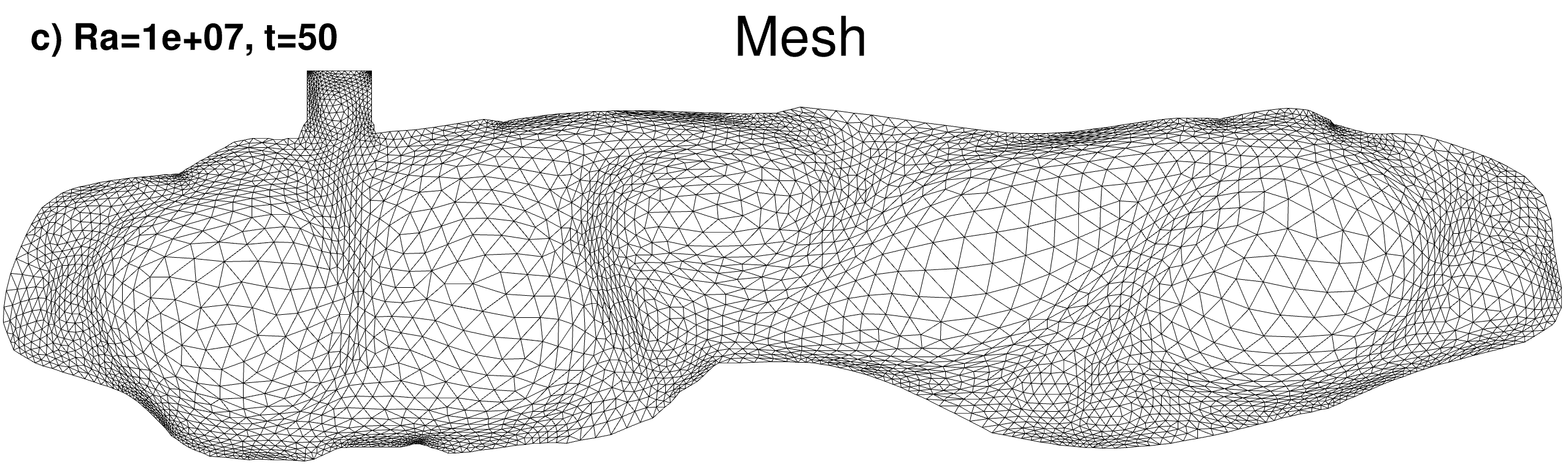 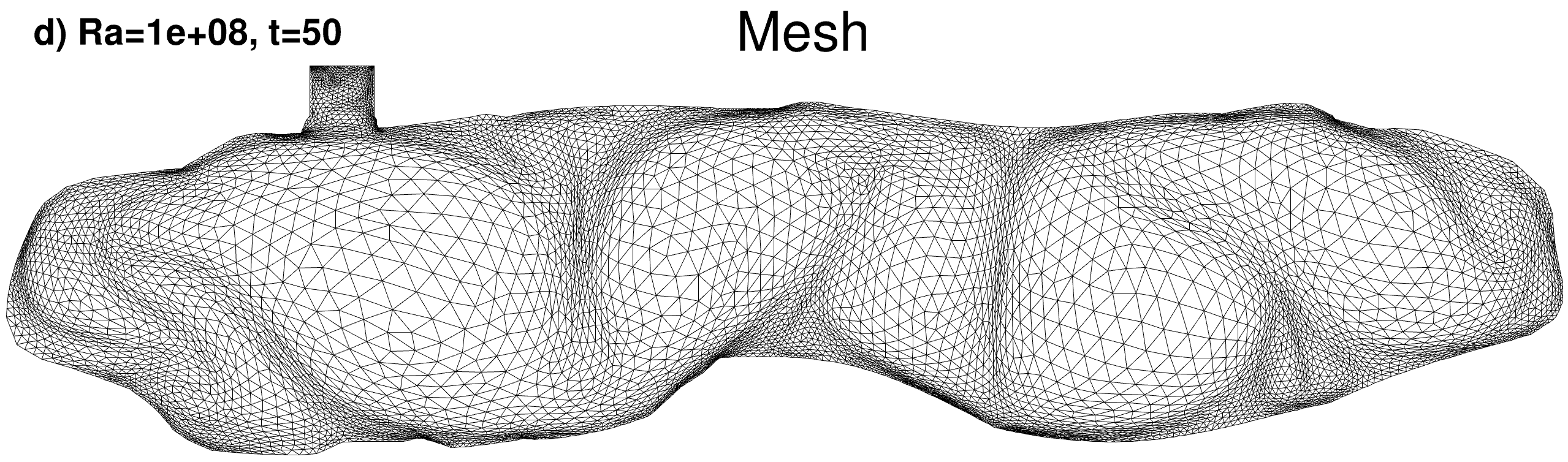 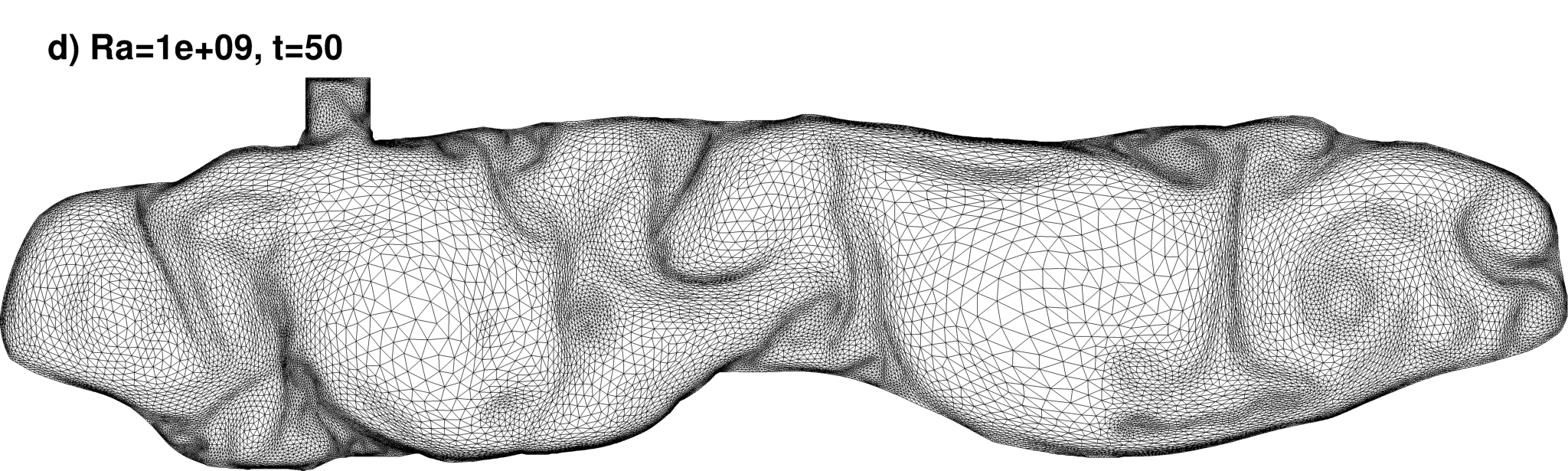
|
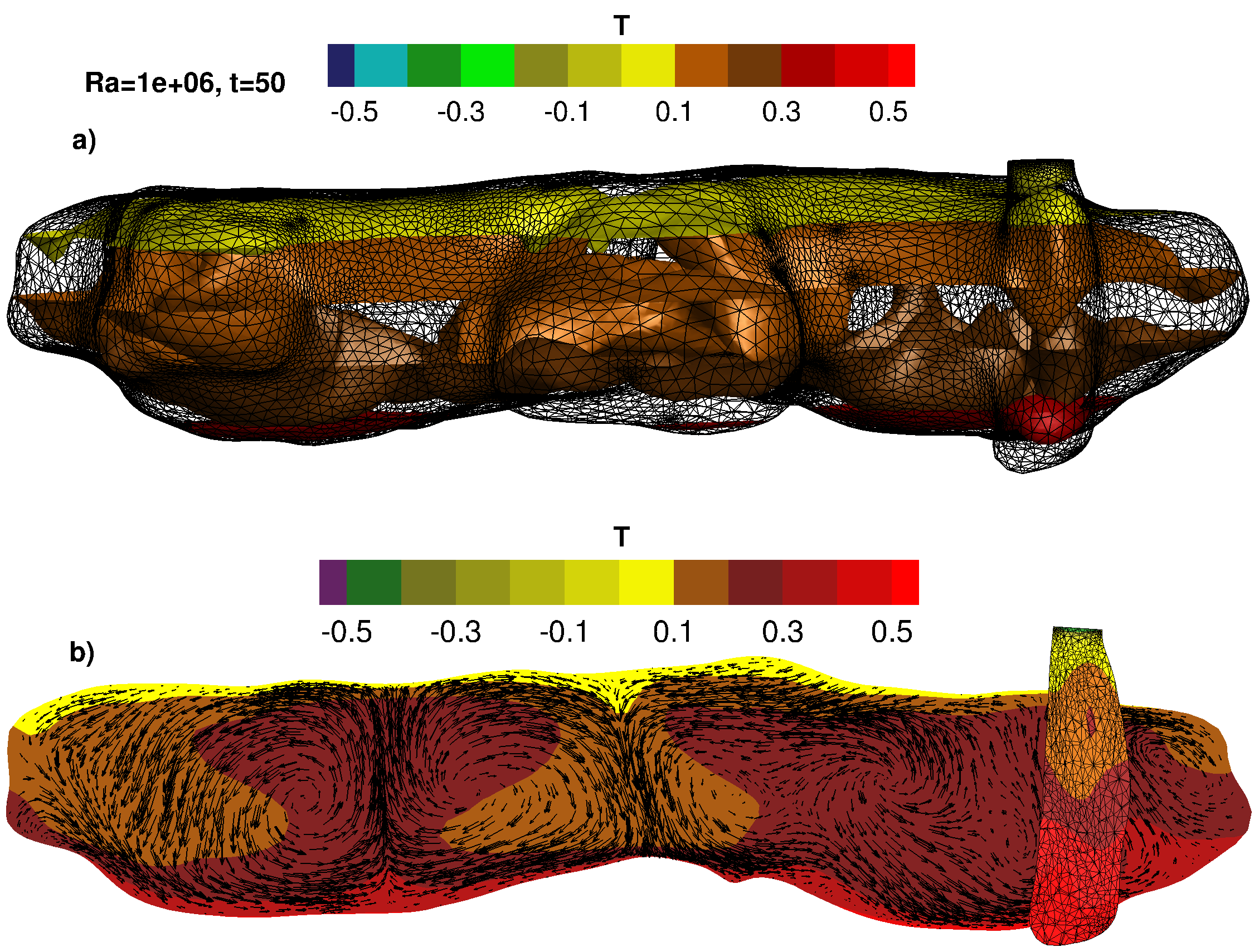
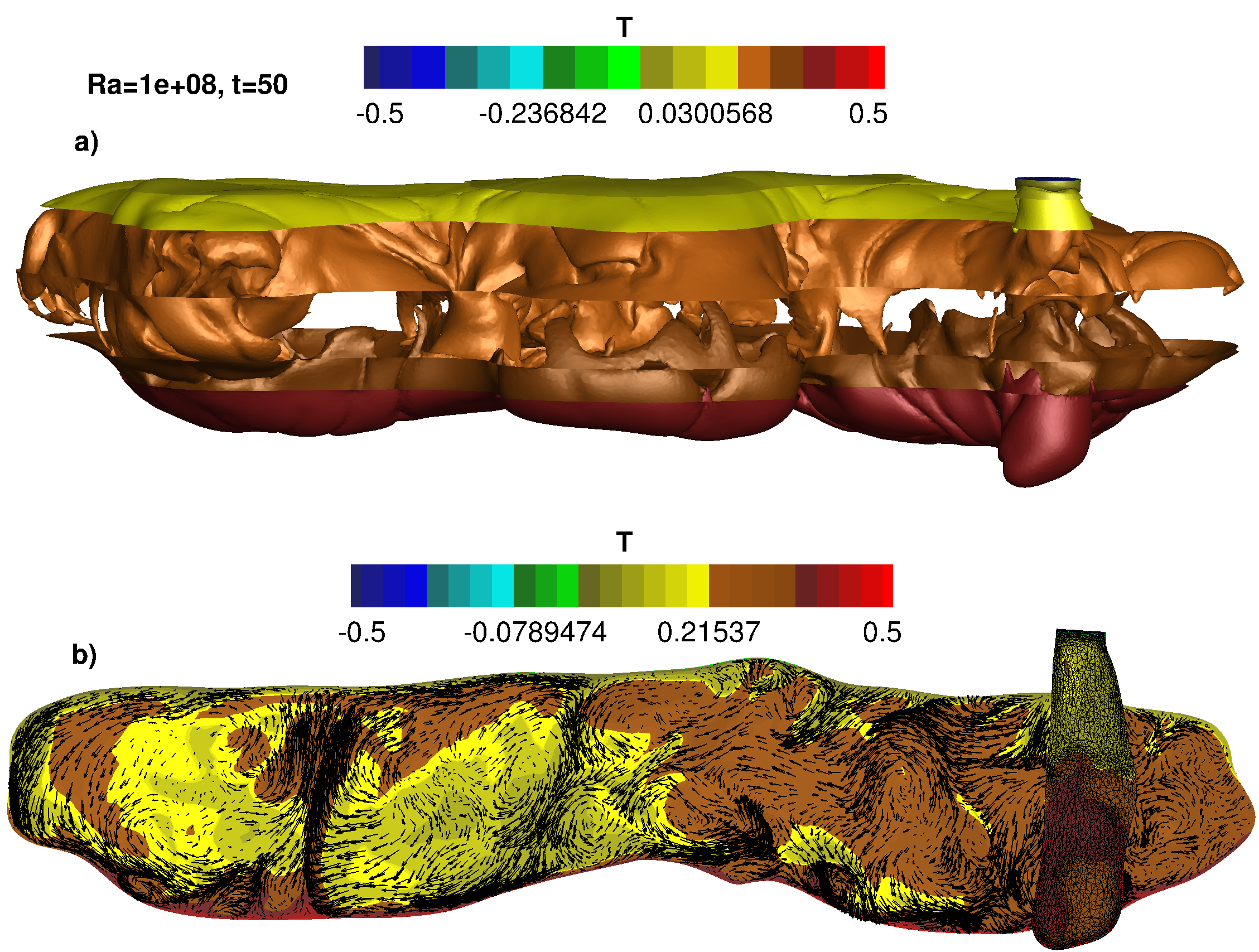
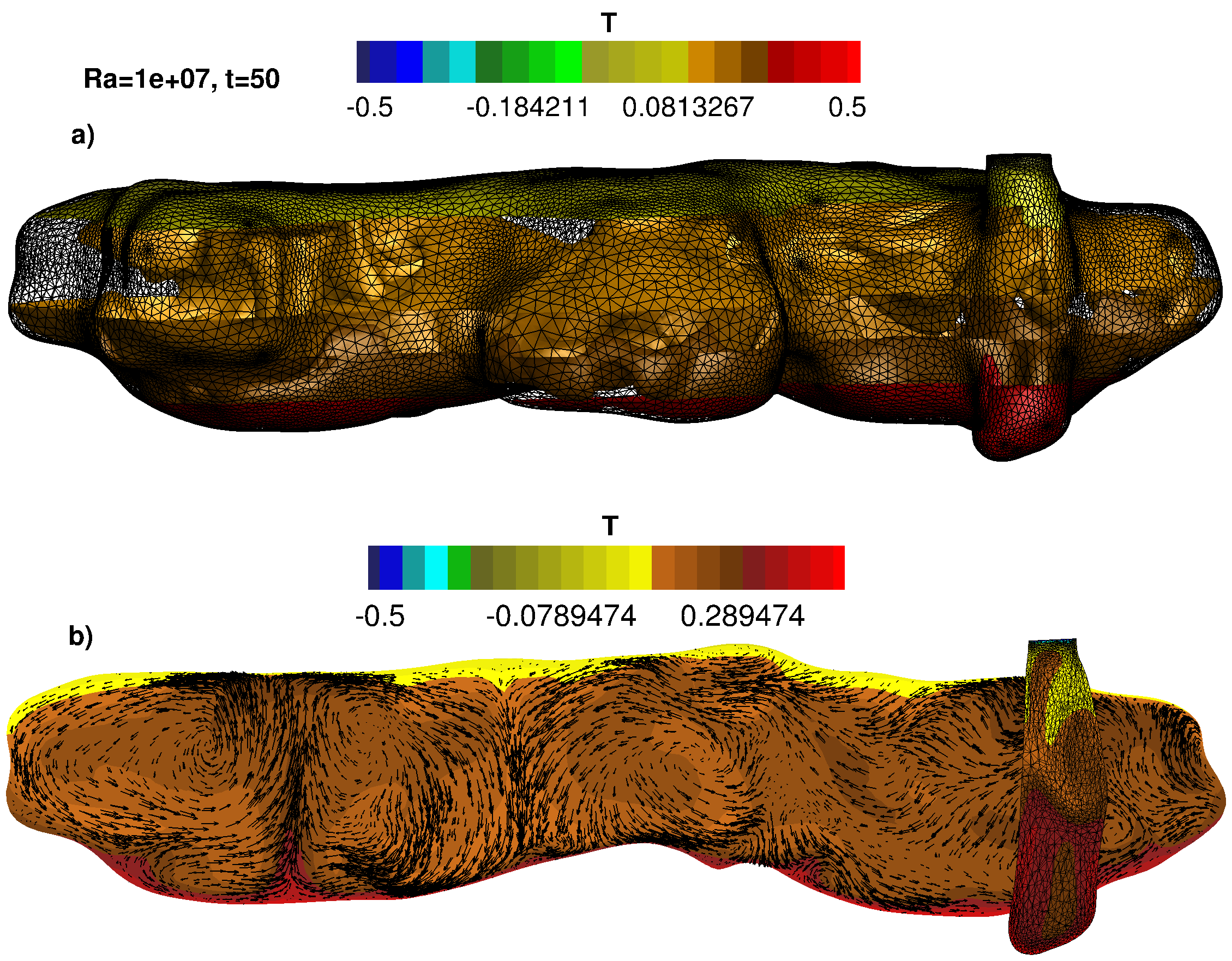
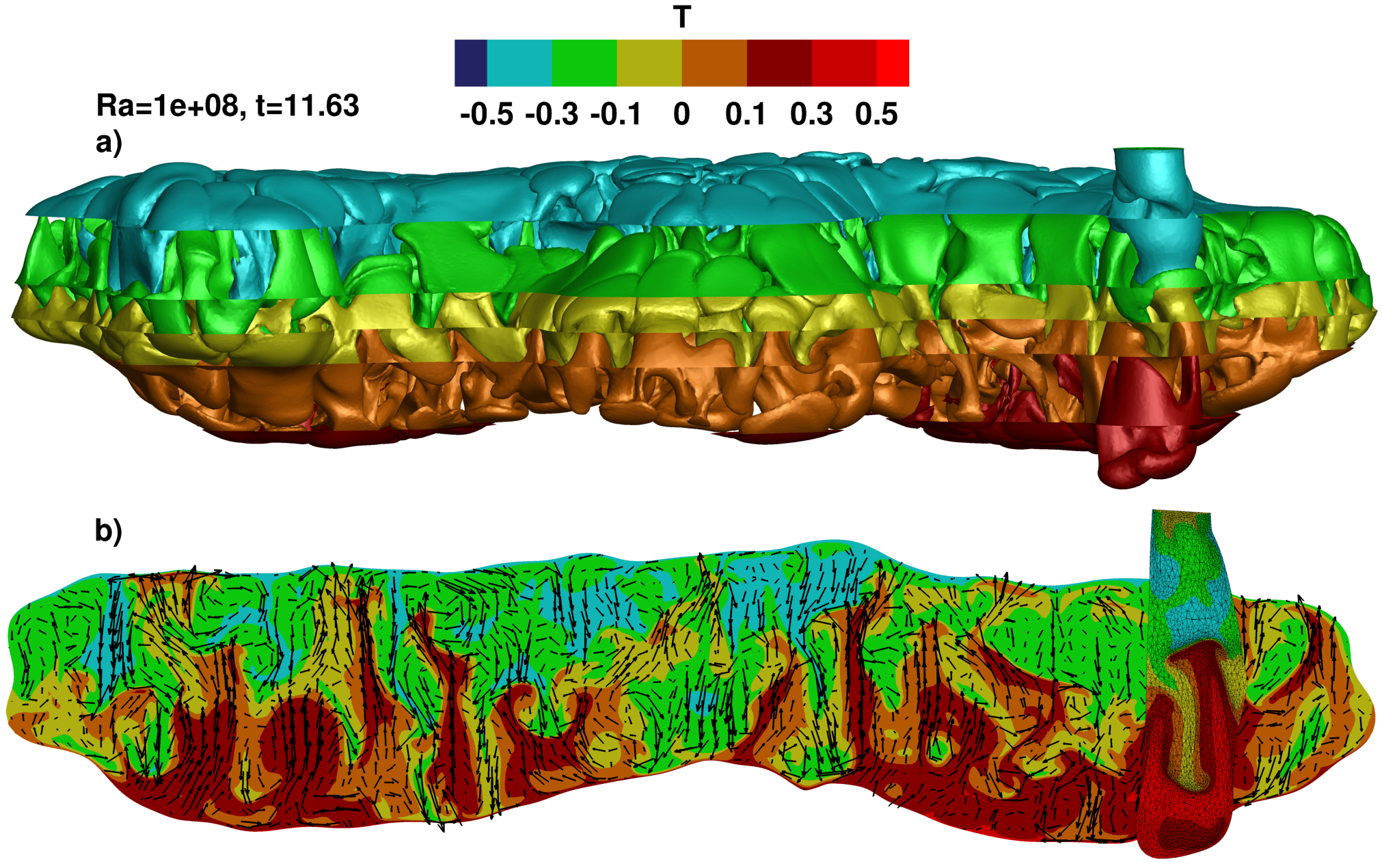
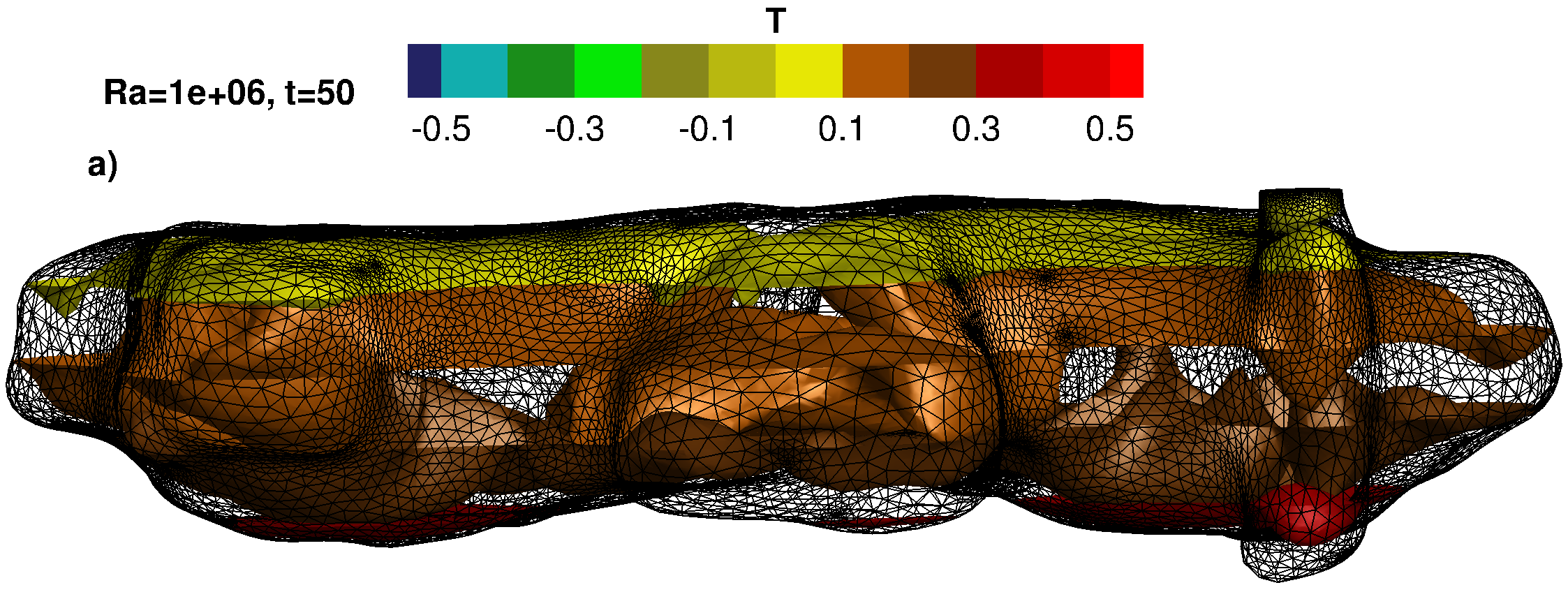
Results for the 3D configuration: a) mesh and five isosurfaces of temperature, b) velocity vectors.
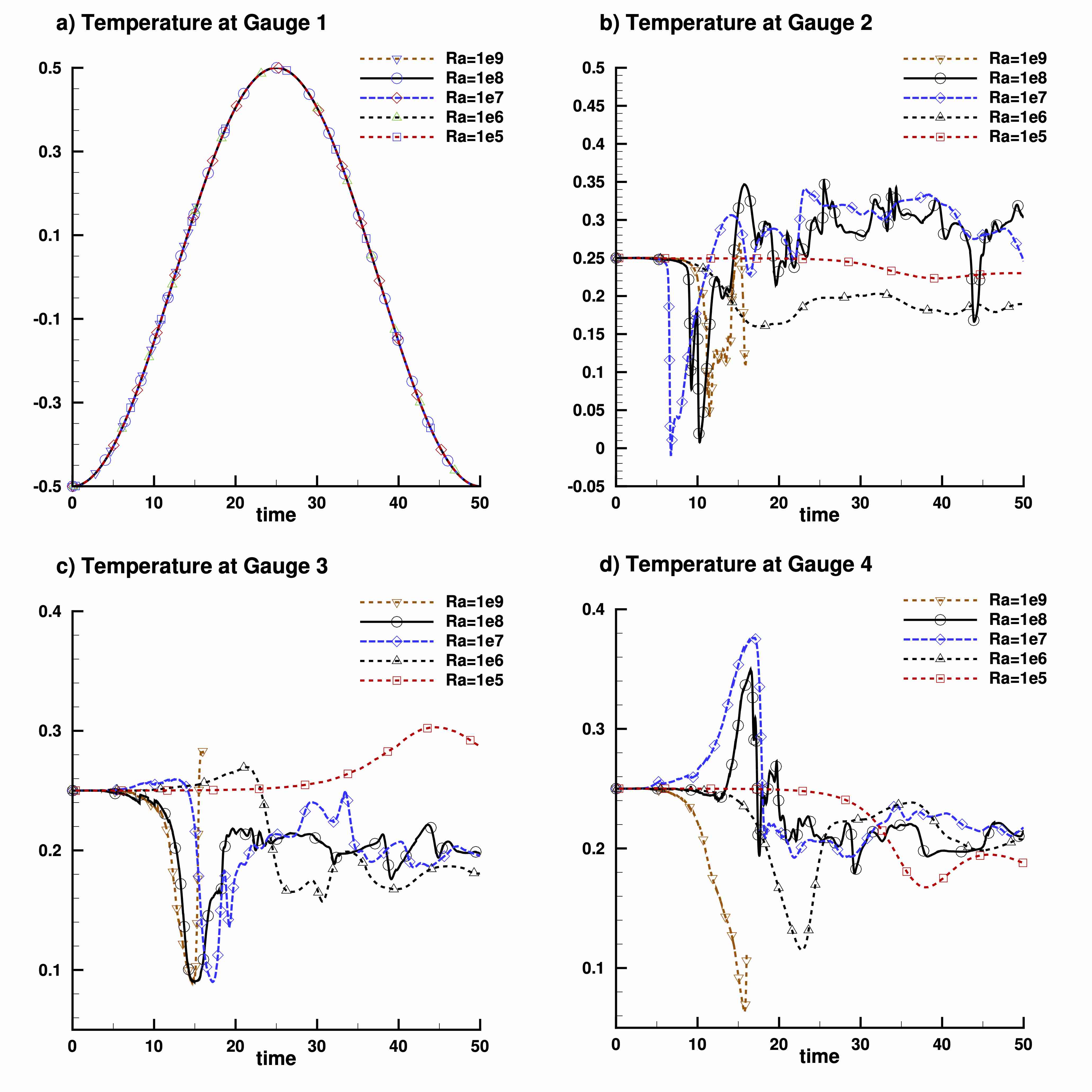
Supplemental material: time evolution of the temperature measured at gauges G1 to G4 for five values of the Rayleigh number
|
|
2D configuration
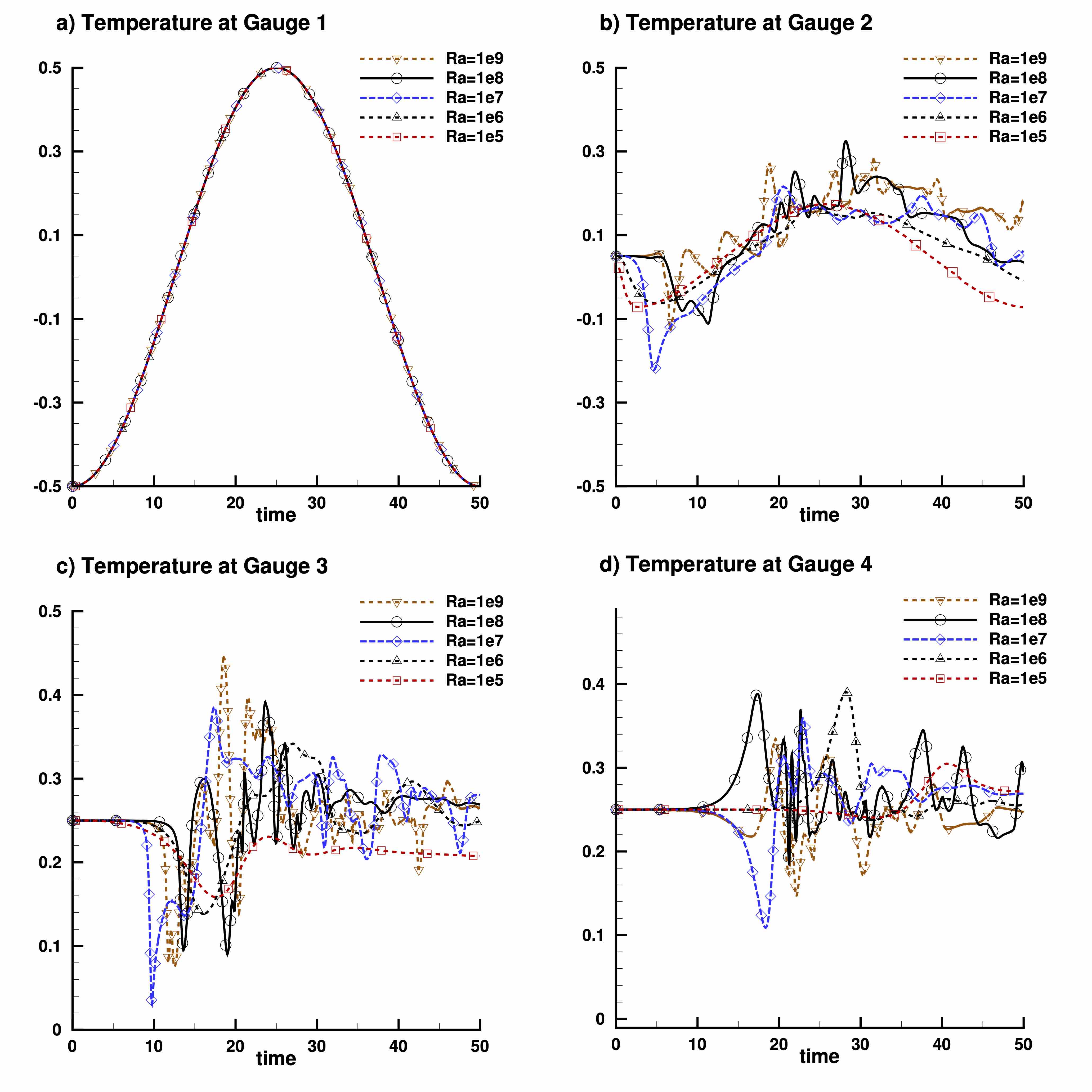
|
3D configuration
|