Download preprint-pdf
Authors
V. Kalt, G. Sadaka, I. Danaila and F. Hecht
Abstract
We present finite-element numerical algorithms for the identification of vortices in quantum fluids described by a macroscopic complex wave function. Their implementation using the free software FreeFem++ is distributed with this paper as a post-processing toolbox that can be used to analyse numerical or experimental data. Applications for Bose-Einstein condensates (BEC) and superfluid helium flows are presented. Programs are tested and validated using either numerical data obtained by solving the Gross-Pitaevskii equation or experimental images of rotating BEC. Vortex positions are computed as topological defects (zeros) of the wave function when numerical data are used. For experimental images, we compute vortex positions as local minima of the atomic density, extracted after a simple image processing. Once vortex centers are identified, we use a fit with a Gaussian to precisely estimate vortex radius. For vortex lattices, the lattice parameter (inter-vortex distance) is also computed. The post-processing toolbox offers a complete description of vortex configurations in superfluids. Tests for two-dimensional (giant vortex in rotating BEC, Abrikosov vortex lattice in experimental BEC) and three-dimensional (vortex rings, Kelvin waves and quantum turbulence fields in superfluid helium) configurations show the robustness of the software. The communication with programs providing the numerical or experimental wave function field is simple and intuitive. The post-processing toolbox can be also applied for the identification of vortices in superconductors.
FreeFem++ Toolbox
Nature of problem: The software is scoped to the identification of quantized vortices in 2D or 3D configurations described by a complex wave function. Either simulation data obtained through numerical resolution of the Gross-Pitaevskii equation or 2D experimental images of Bose-Einstein condensates (BEC) can be used as input data. Examples of vortex identification in rotating BECs and superfluid helium are illustrated in the paper.
Solution method: We model the complex wave function using P1 (piece-wise linear) Galerkin triangular (in 2D) and tetrahedral (in 3D) finite elements. For simulation data, the zeros of the wave function are directly computed and the circulation of the velocity on triangles sides is assessed. Vortices are obtained when a zero is found in a triangle with non-zero circulation. In 3D, the algorithm is applied on tetrahedron faces and the zero points are linked using mesh connectivity to form vortex lines. For experimental images, vortices are identified as local minima of the atomic density and extracted using the image contrast.
Running time: Running time is from seconds to minutes depending on the mesh resolution of the simulation/experimental data.
Supplemental material: vortex identification in 2D
| Numerical or experimental density | Illustration of vortex identification |
|---|---|
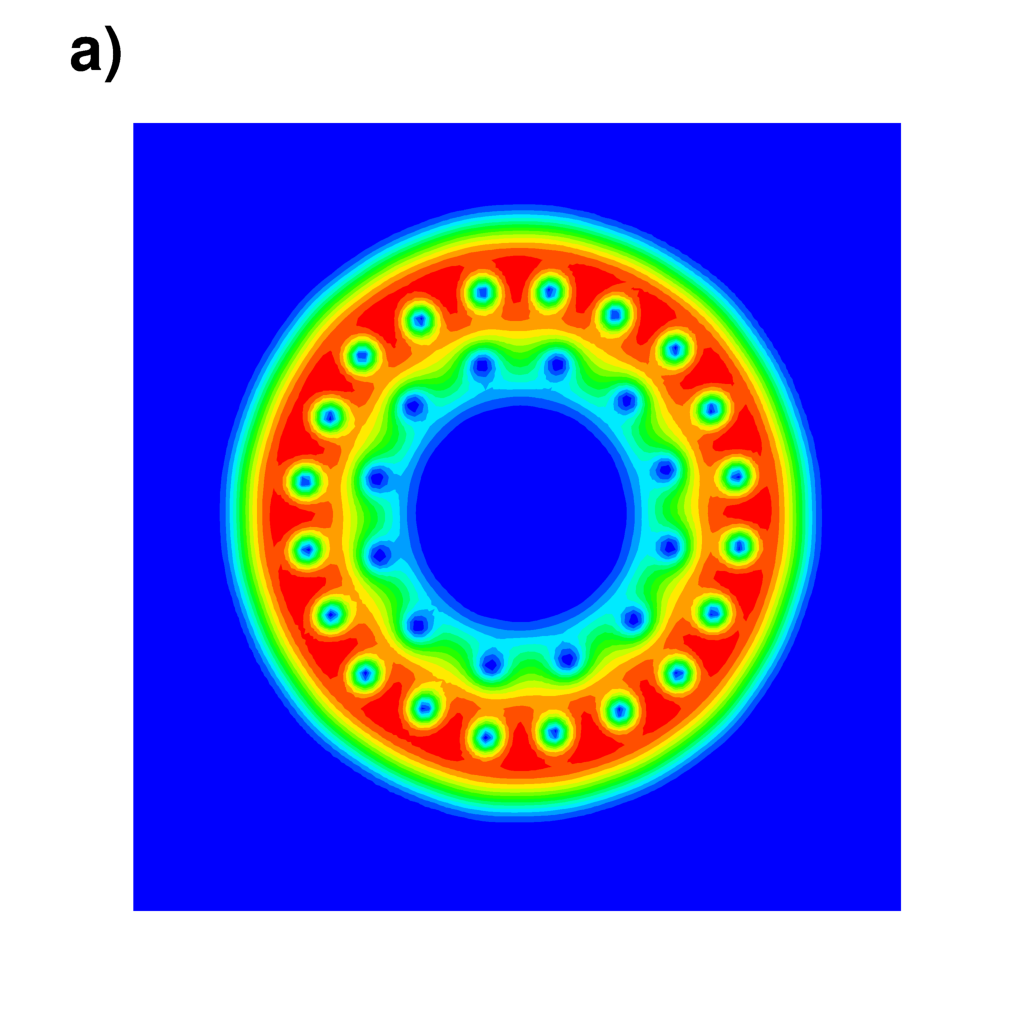
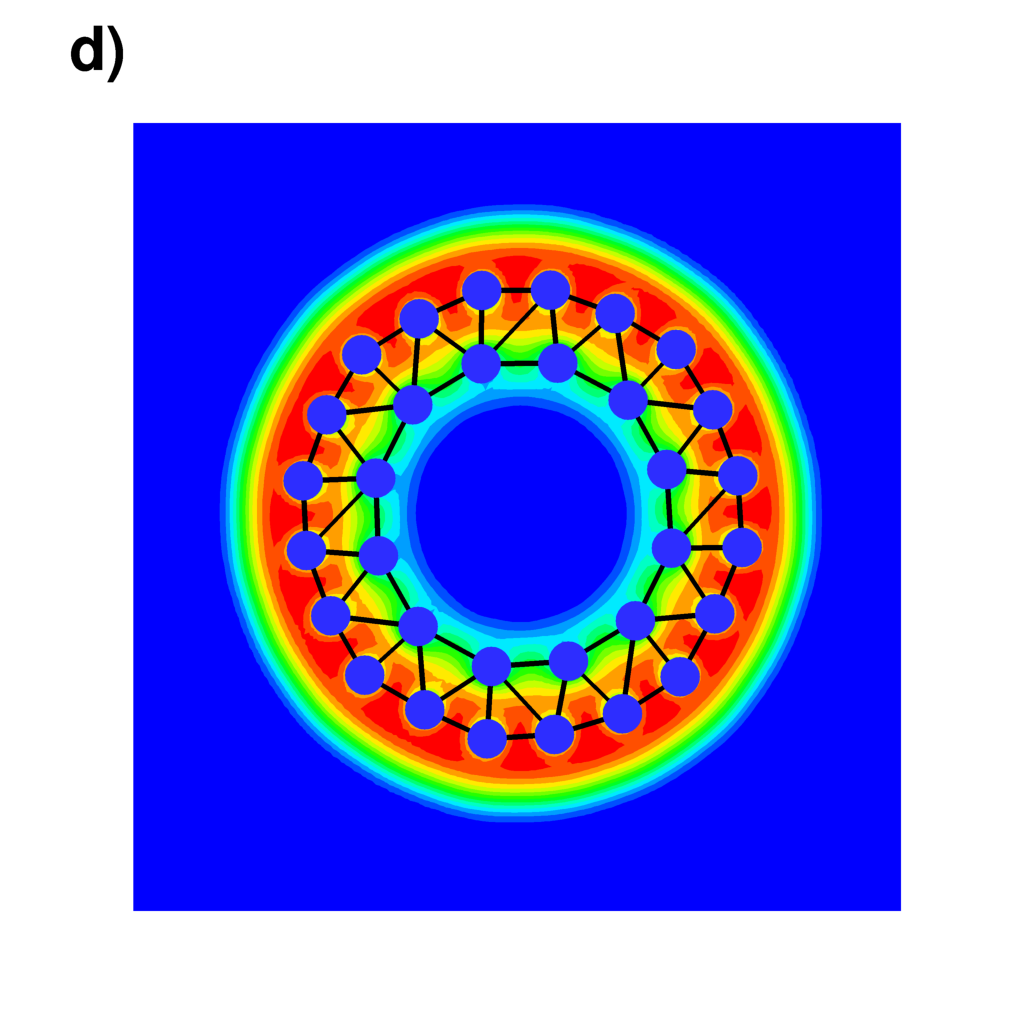
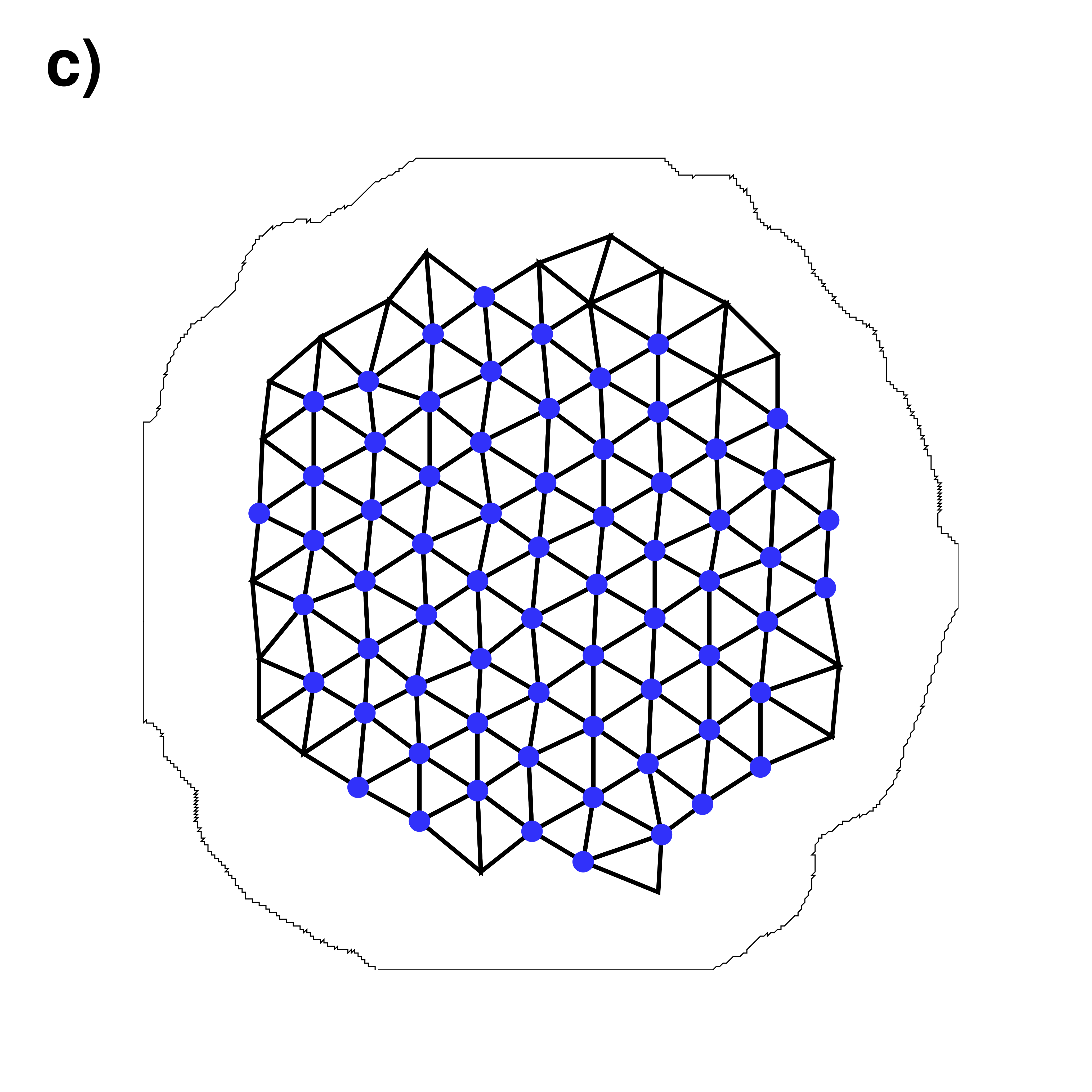
| Numerical simulation of a fast rotating BEC with a quartic-minus-quadratic trapping potential | |
Density
 |
Mesh of the identified vortex lattice (blue points)
 |
| Numerical simulation of a dense Abrikosov lattice in fast rotating BEC. Wave function field obtained with a spectral GP code | |
Density
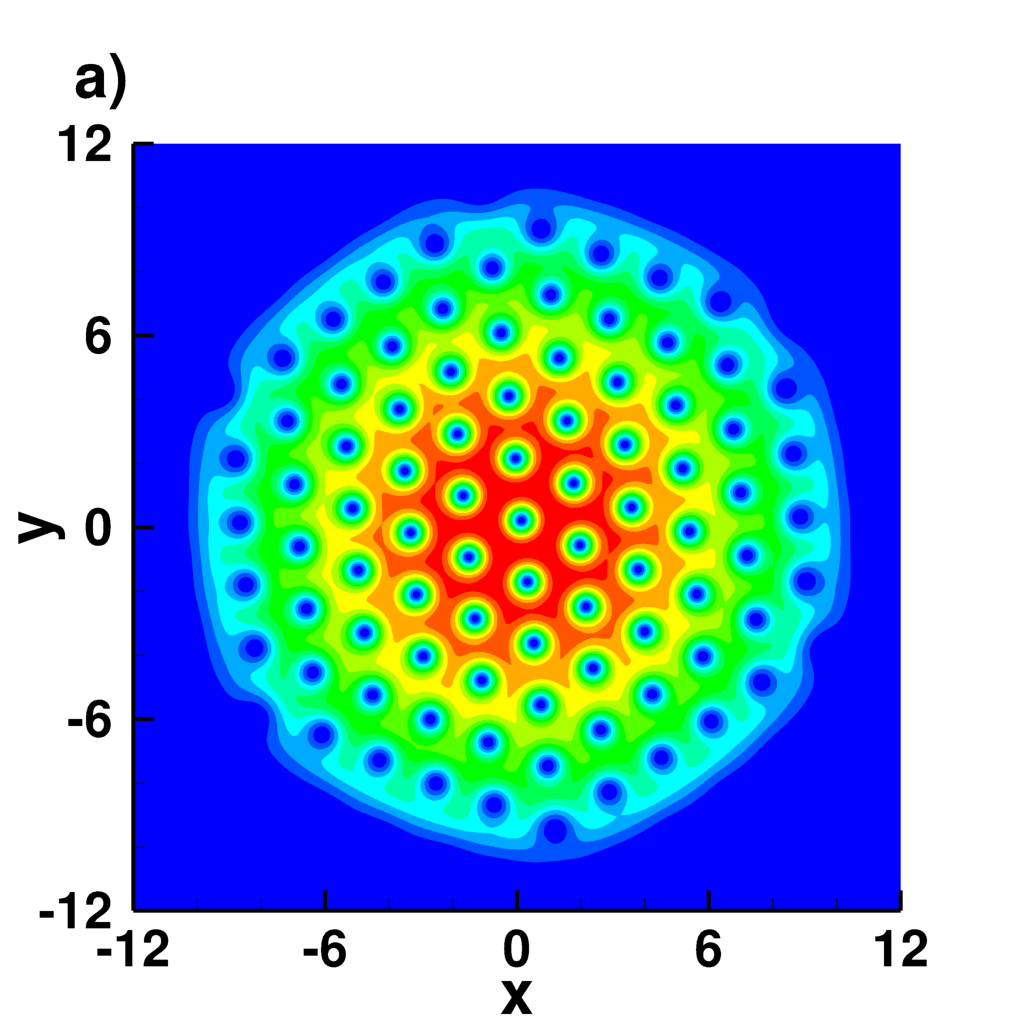 |
Mesh of the identified vortex lattice (blue points)
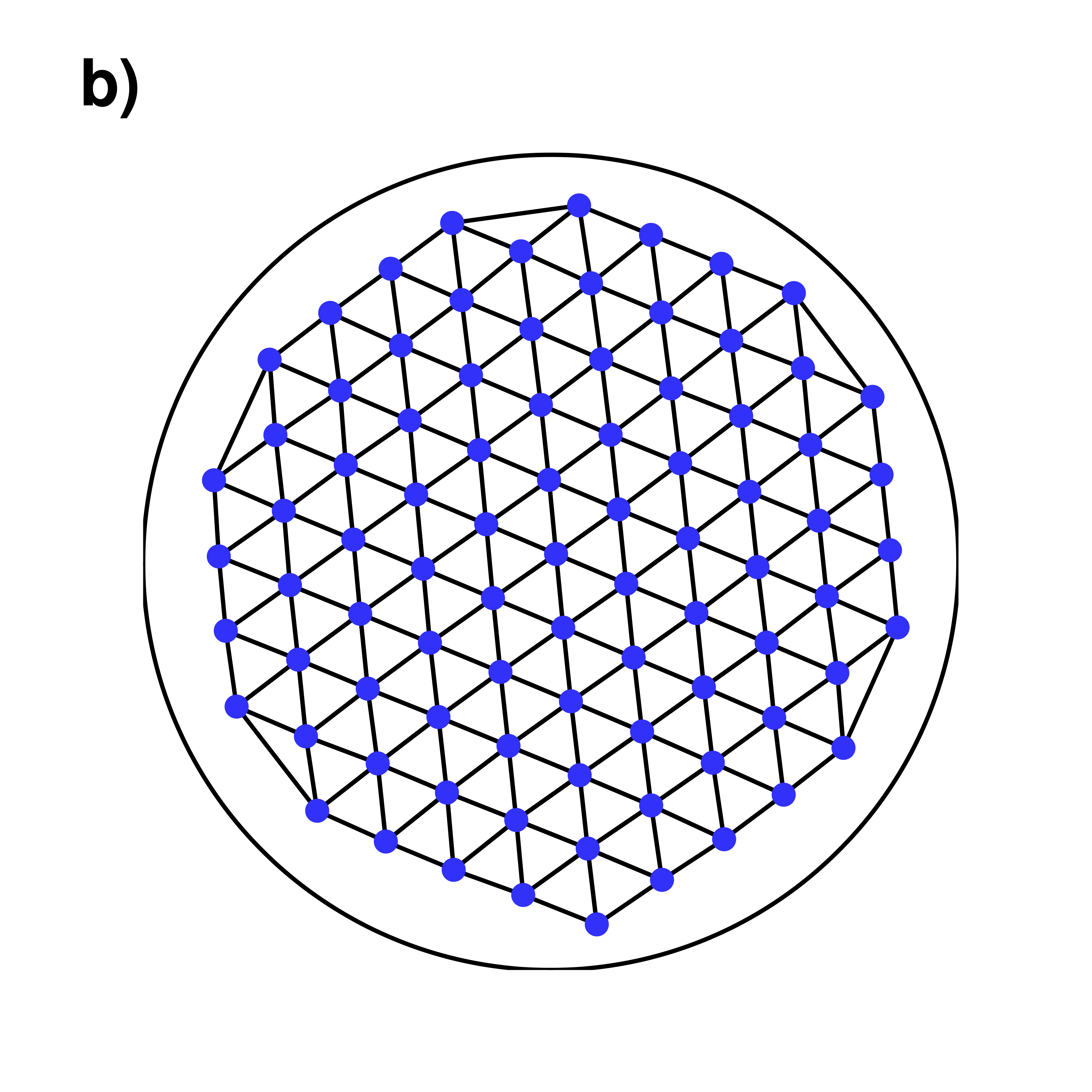 |
| Experimental simulation of a vortex lattice in a slowly rotating BEC | |
Experimental image of atomic density
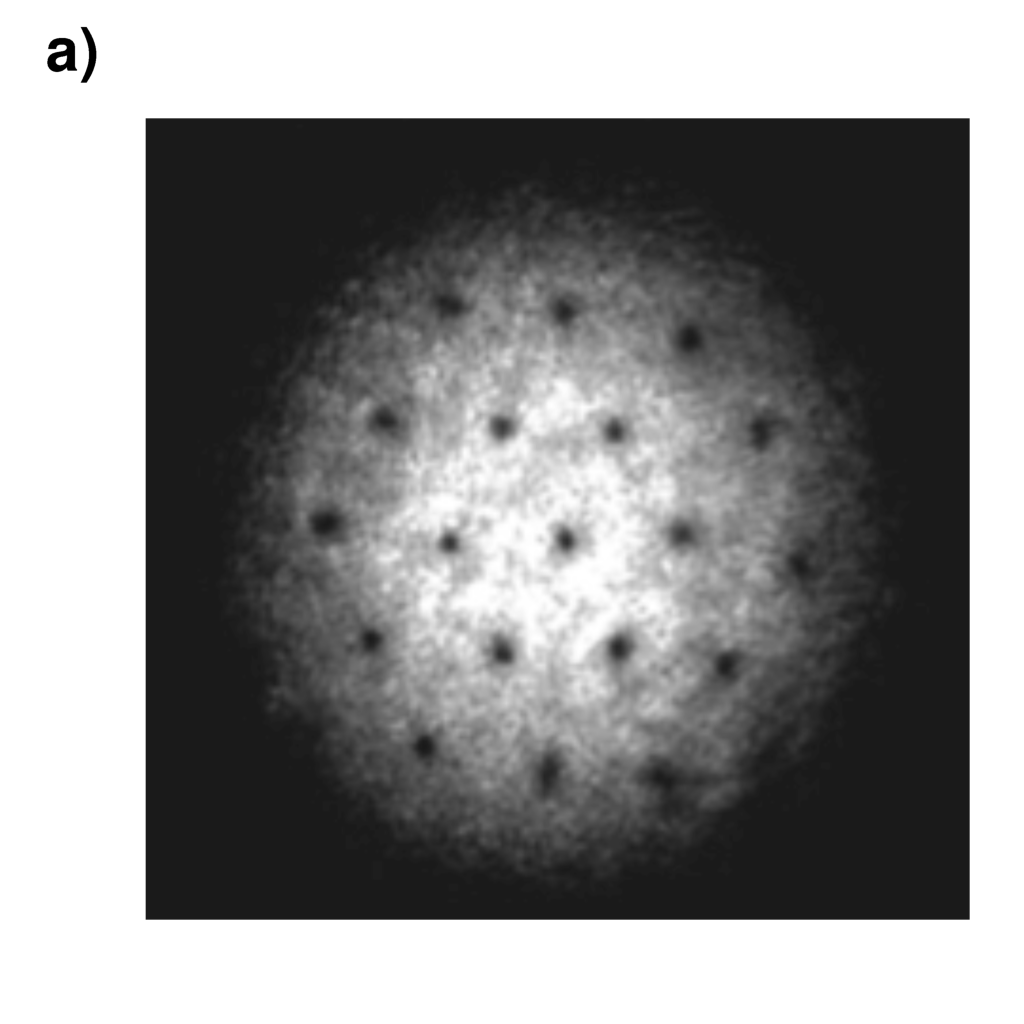 |
Mesh of the identified vortex lattice (blue points)
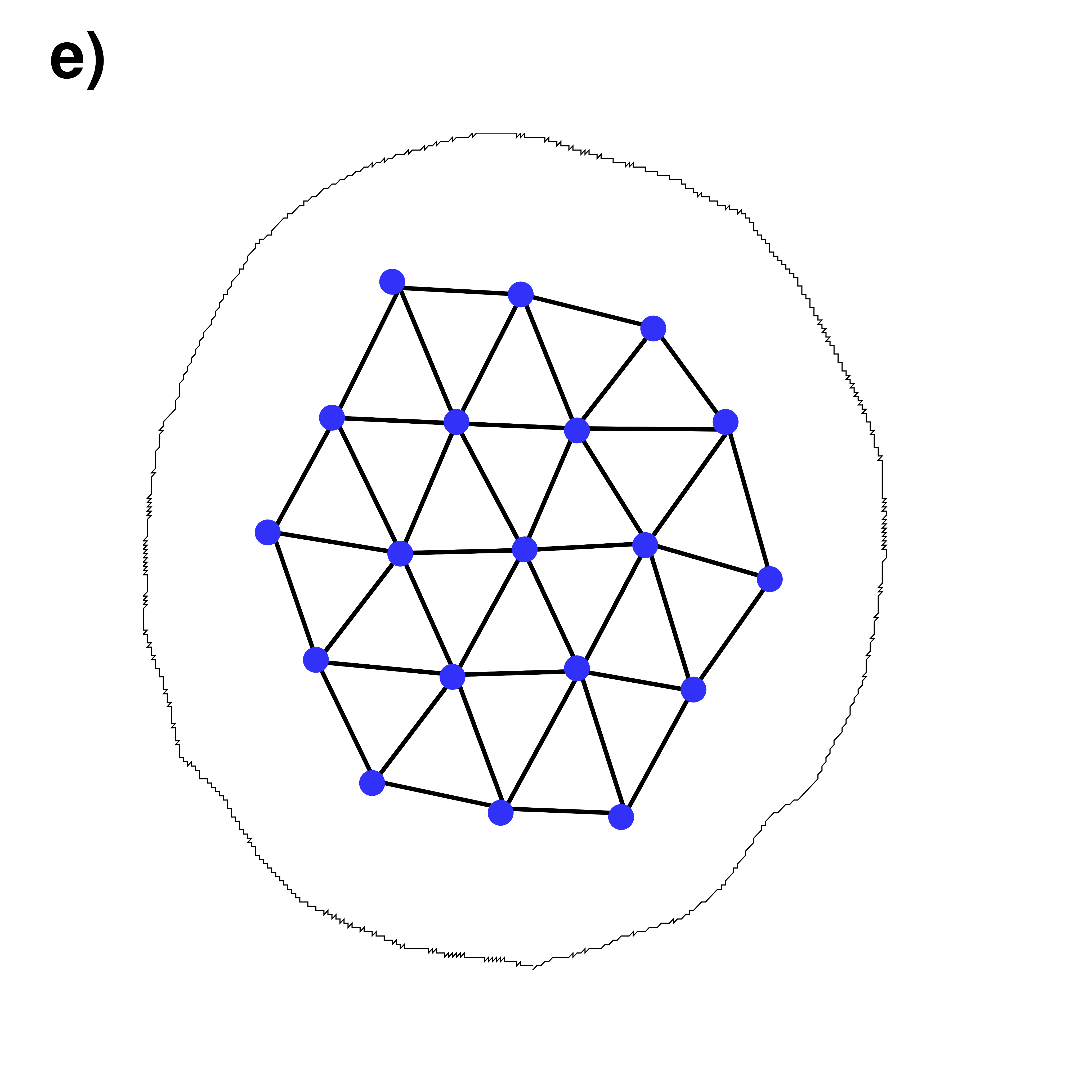 |
| Experimental simulation with a dense Abrikosov vortex lattice | |
Experimental image of atomic density
 |
Mesh of the identified vortex lattice (blue points)
 |
Supplemental material: vortex line identification in 3D
| Numerical density | Illustration of vortex line identification |
|---|---|
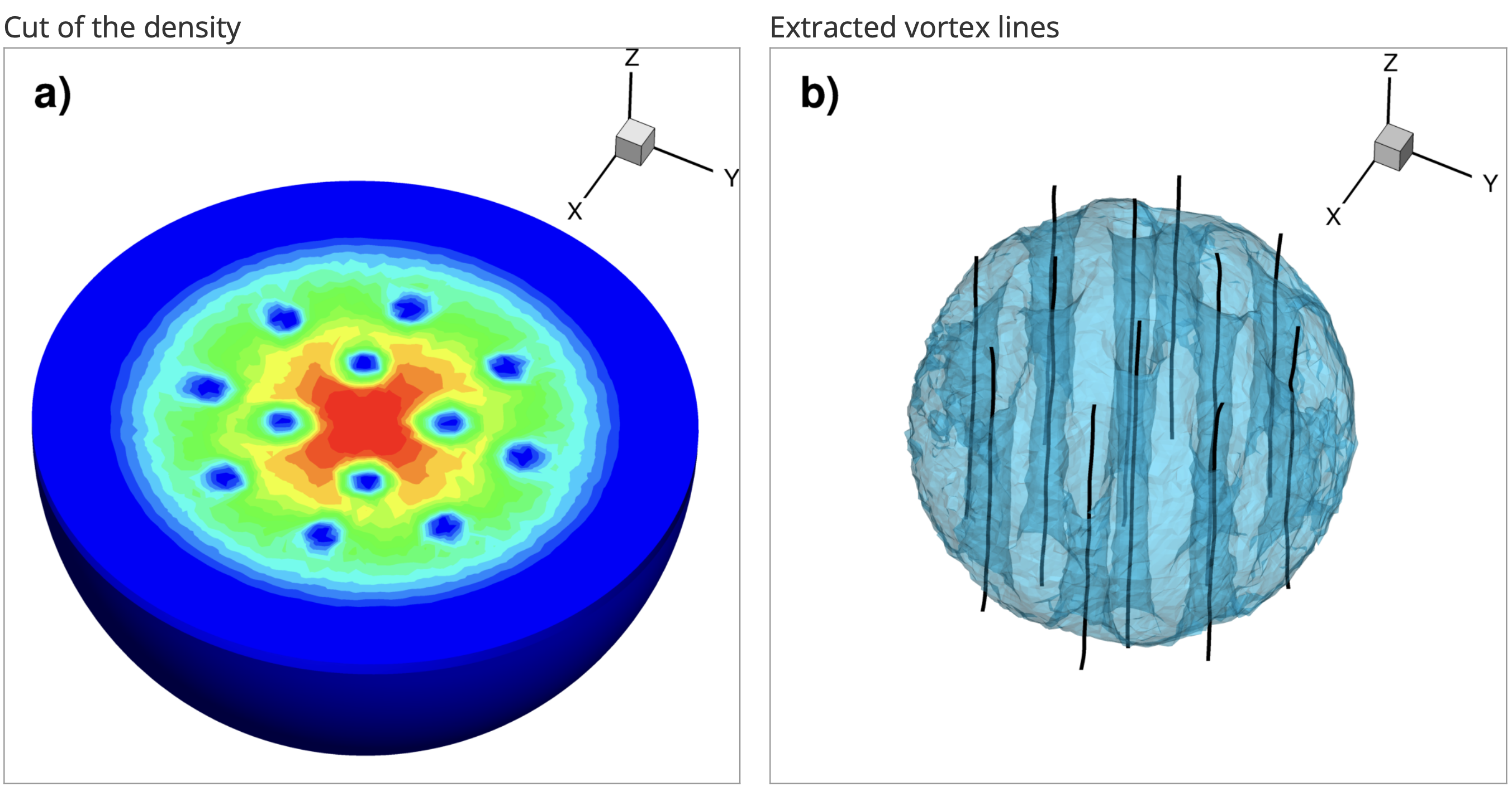
| Numerical simulation of a rotating BEC obtained on an unstructured mesh using a finite-element solver | |
Cut of the density
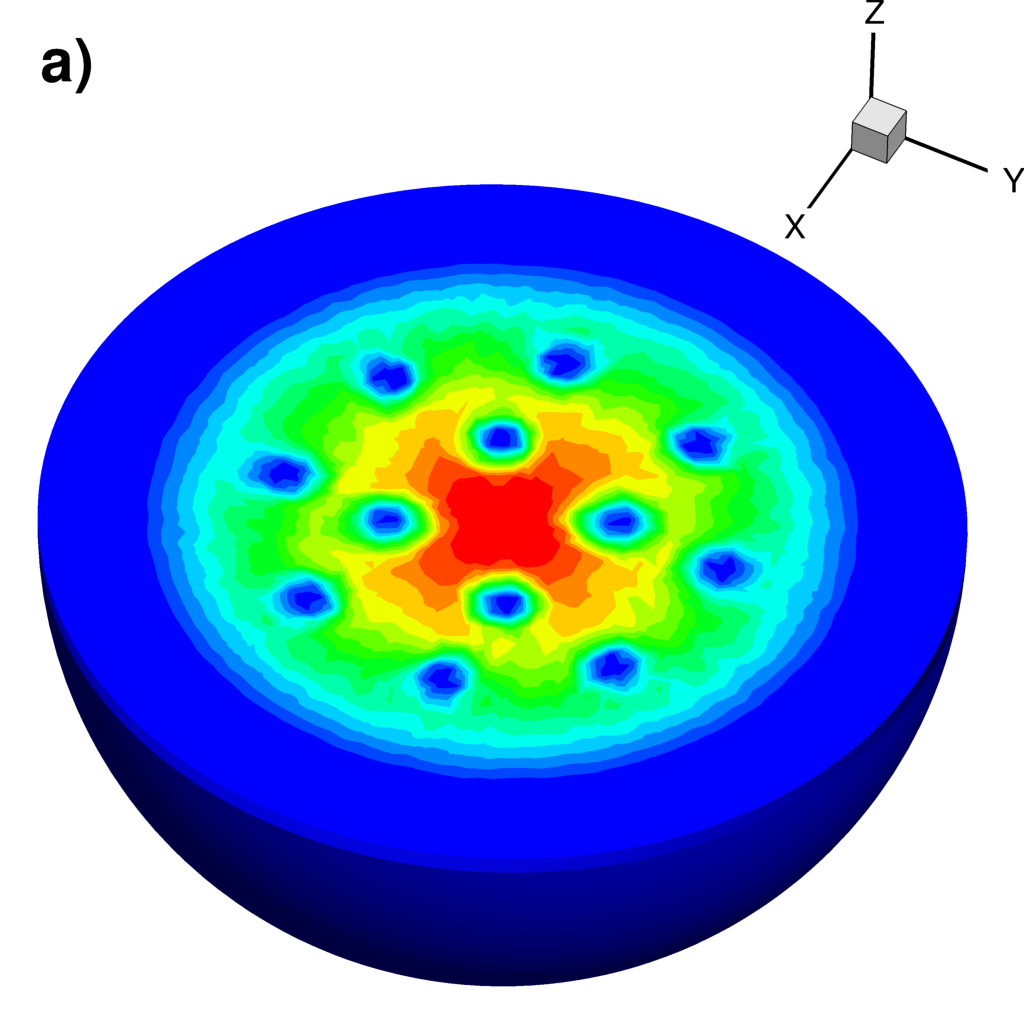 |
Extracted vortex lines
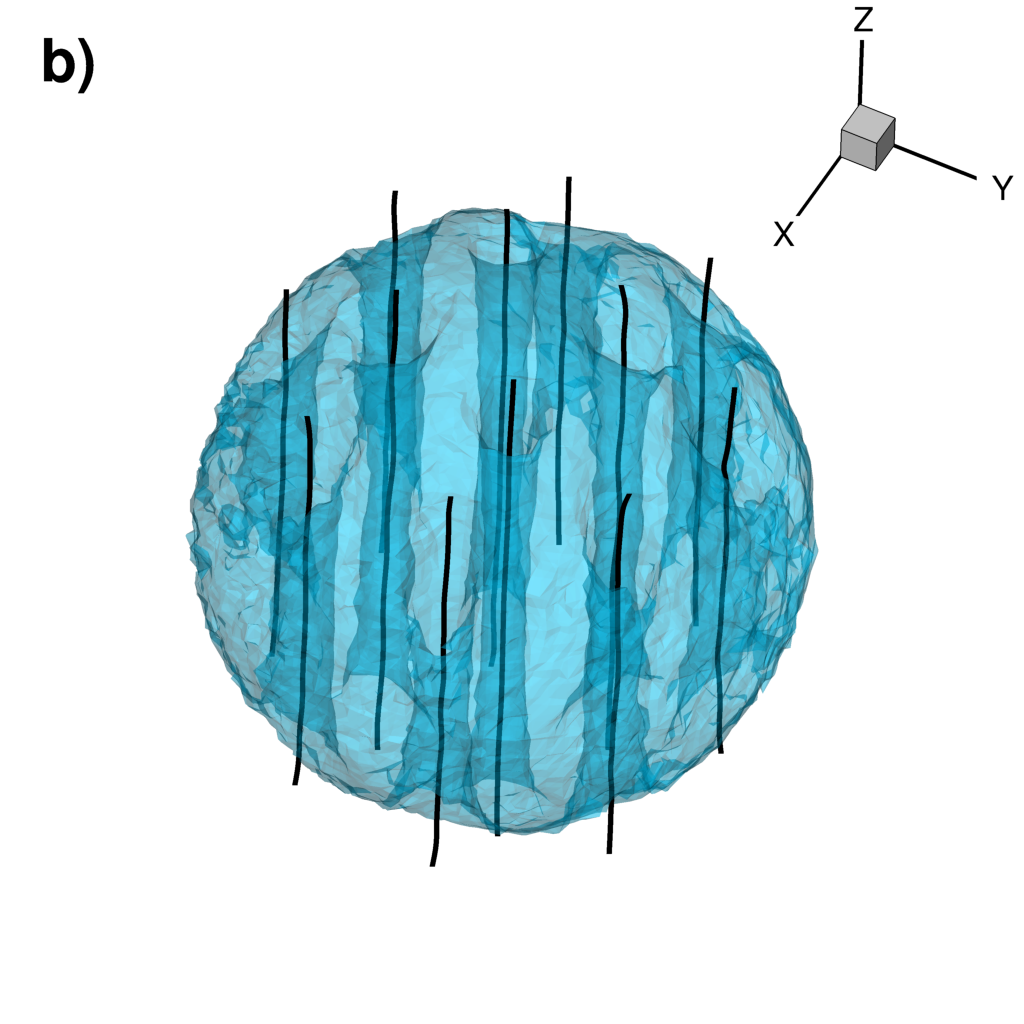 |
| Numerical simulation of for quantum turbulence in superfluid helium. Spectral numerical simulation of the GP equation | |
Tetrahedrons with non-zero circulation
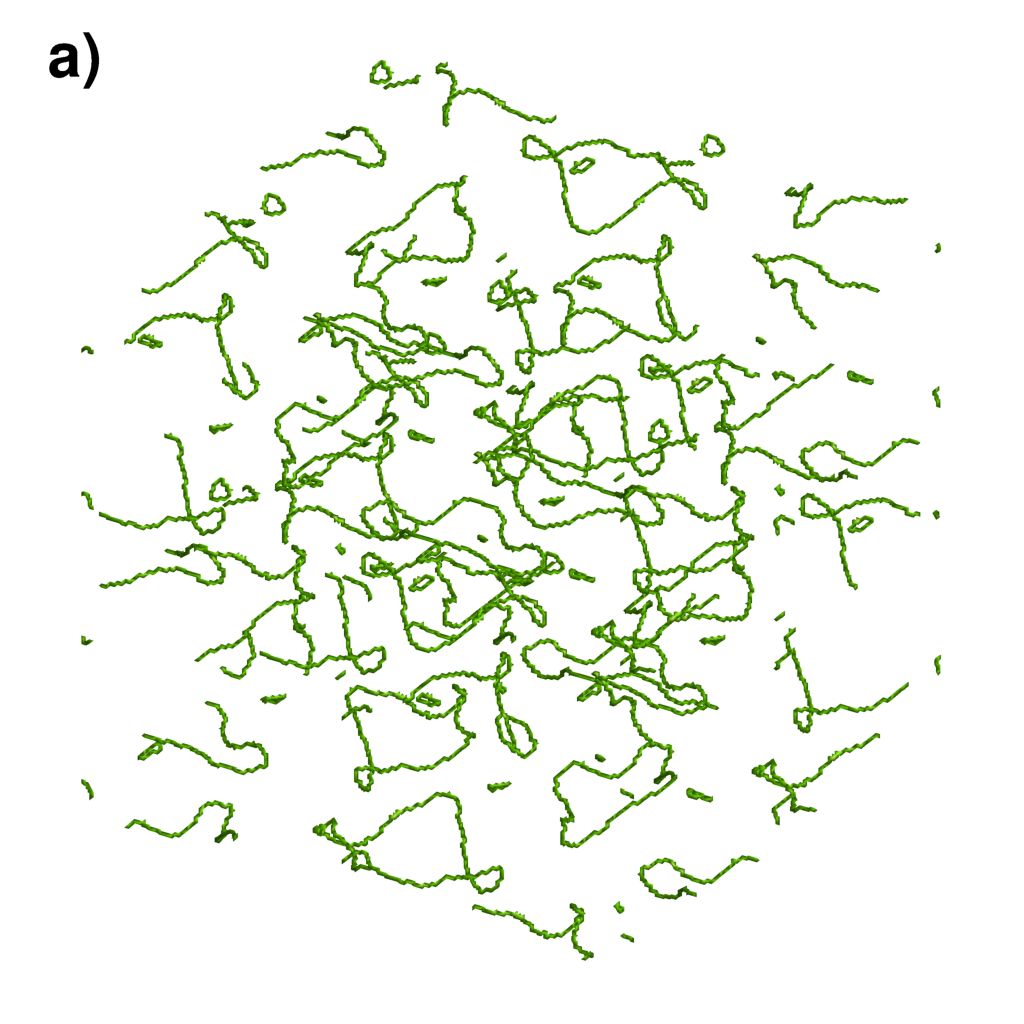 |
Identified vortex lines with resolution $128^3$
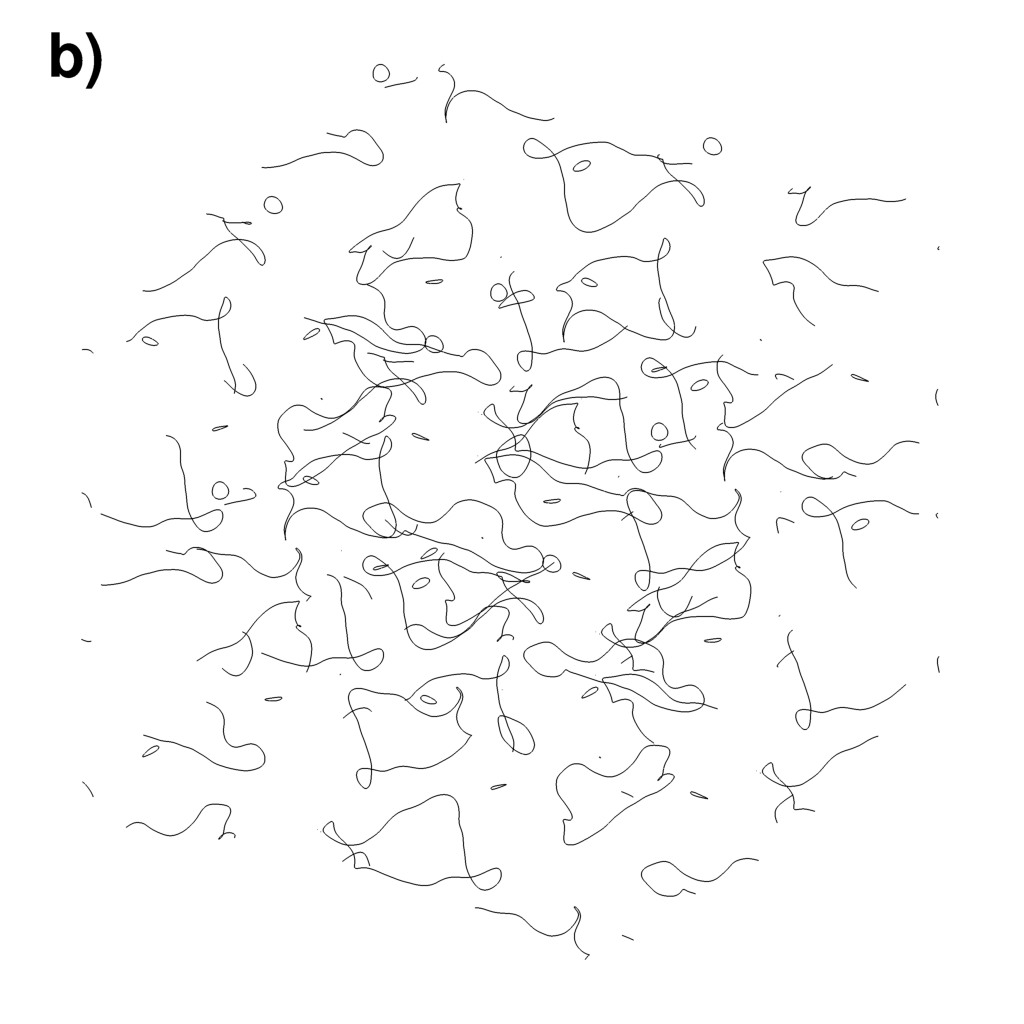 |
Tetrahedrons with non-zero circulation
 |
Identified vortex lines with resolution $256^3$
 |
