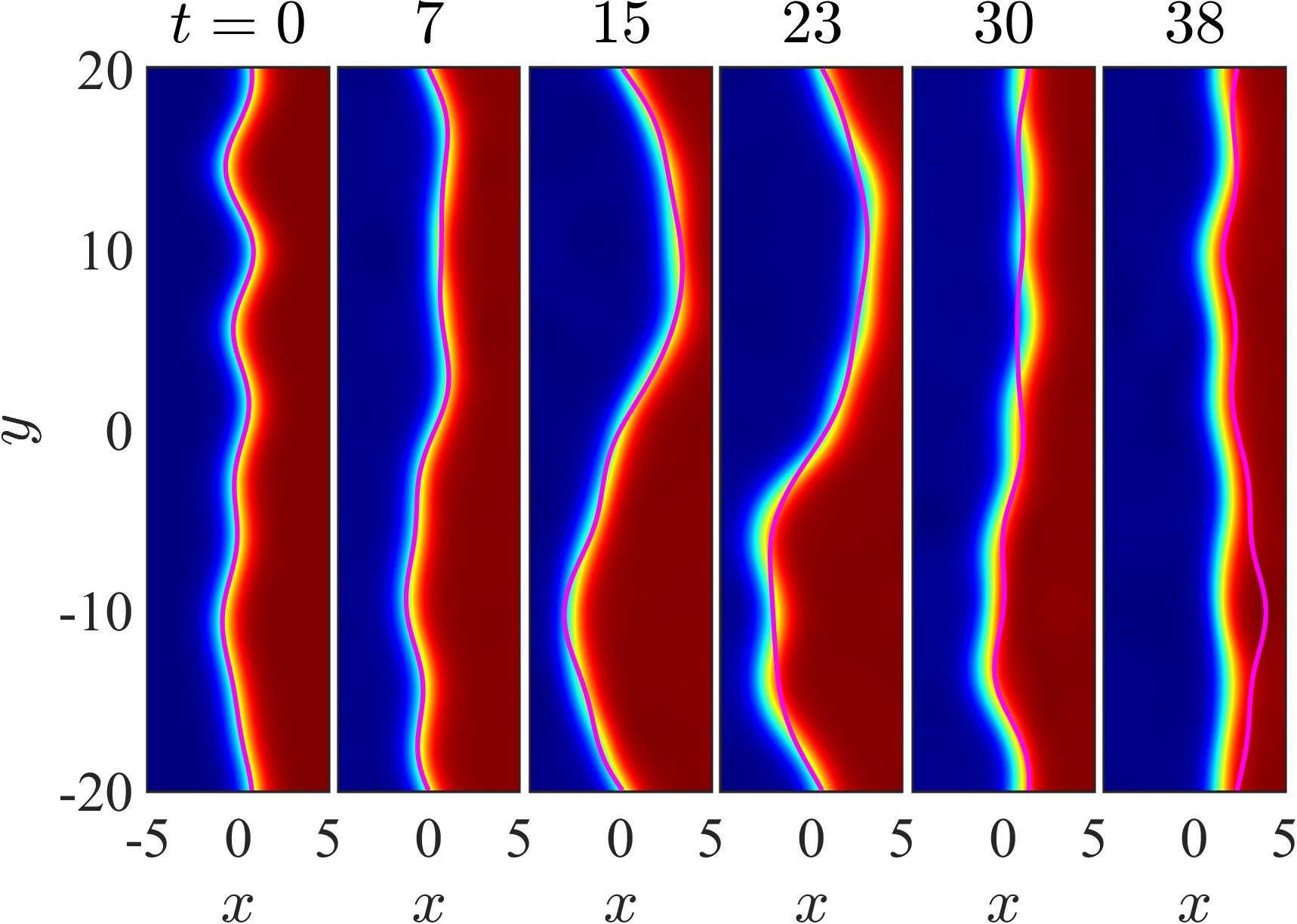
We consider effectively one-dimensional planar and radial kinks in two-dimensional nonlinear Klein-Gordon models and focus on the sine-Gordon model and the $\phi^4$ variants thereof. We adapt an adiabatic invariant formulation recently developed for nonlinear Schrödinger equations, and we study the transverse stability of these kinks. This enables us to characterize one-dimensional planar kinks as solitonic filaments, whose stationary states and corresponding spectral stability can be characterized not only in the homogeneous case, but also in the presence of external potentials. Beyond that, the full nonlinear (transverse) dynamics of such filaments are described using the reduced, one-dimensional, adiabatic invariant formulation. For radial kinks, this approach confirms their azimuthal stability. It also predicts the possibility of creating stationary and stable ring-like kinks. In all cases we corroborate the results of our methodology with full numerics on the original sine-Gordon and $\phi^4$ models.